Условие фано для построения оптимального кода. Условие фано. Практическое применение условия Фано

Лекция 3. Общие теоремы динамики

Динамика системы материальных точек является важным разделом теоретической механики. Здесь в основном рассматриваются задачи о движении механических систем (систем материальных точек) с конечным числом степеней свободы – максимальным числом независимых параметров, определяющих положение системы. Главная задача динамики системы – изучение законов движения твердого тела и механических систем.

Наиболее простой подход к исследованию движения системы, состоящий из N материальных точек, сводиться к рассмотрению движений каждой отдельной точки системы. При этом должны быть определены все силы, действующие на каждую точку системы, в том числе и силы взаимодействия между точками.

Определяя ускорения каждой точки в соответствии со вторым законом Ньютона (1.2), получим для каждой точки три скалярных дифференциальных закона движения второго порядка, т.е. 3 N дифференциальных закона движения для всей системы.

Для нахождения уравнений движения механической системы по заданным силам и начальным условиям для каждой точки системы, полученные дифференциальные законы нужно проинтегрировать. Эта задача трудна даже в случае двух материальных точек, которые движутся только под действием сил взаимодействия по закону всемирного притяжения (задача о двух телах), и исключительно трудна в случае трех взаимодействующих точек (задача о трех телах).

Поэтому необходимо отыскать такие методы решения задач, которые бы приводили к решаемым уравнениям и давали представление о движении механической системы. Общие теоремы динамики, являясь следствием дифференциальных законов движения, позволяют избежать сложности, возникающие при интегрировании и получать необходимые результаты.

3. 1. Общие замечания

Точки механической системы будем нумеровать индексами i , j , k и т.д., которые пробегают все значения 1, 2, 3… N , где N – число точек системы. Физические величины, относящиеся к k -й точке, обозначаются таким же индексом, что и точка. Например, выражают соответственно радиус-вектор и скорость k -й точки.

На каждую из точек системы действуют силы двоякого происхождения: во-первых, силы, источники которых лежат вне системы, называемые внешними силами и обозначаемые ; во-вторых, силы со стороны других точек данной системы, называемые внутренними силами и обозначаемые . Внутренние силы удовлетворяют третьему закону Ньютона. Рассмотрим простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии.

Первое свойство. Геометрическая сумма всех внутренних сил системы (главный вектор внутренних сил) равна нулю .

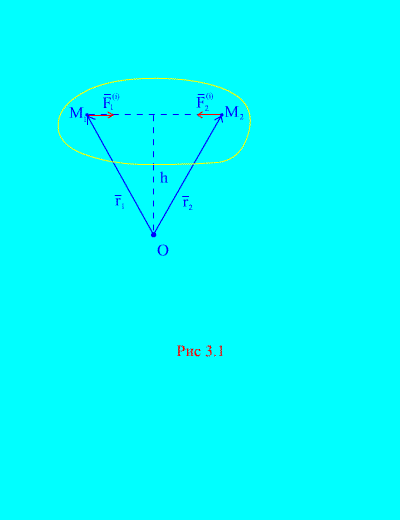
Действительно, если рассмотреть какие-либо две произвольные точки системы, например и (рис. 3.1) , то для них , т.к. силы действия и противодействия всегда равны по модулю, действуют вдоль одной линии действия в противоположном направлении, которое соединяет взаимодействующие точки. Главный вектор внутренних сил состоит из пар сил взаимодействующих точек, следовательно

(3.1)

Второе свойство. Геометрическая сумма моментов всех внутренних сил относительно произвольной точки пространства равна нулю .

Рассмотрим систему моментов сил и относительно точки О (рис. 3.1) . Из (рис. 3.1) . видно, что

,

т.к. обе силы имеют одинаковые плечи и противоположные направления векторных моментов. Главный момент внутренних сил относительно точки О состоит из векторной суммы таких выражений и равен нулю. Следовательно,

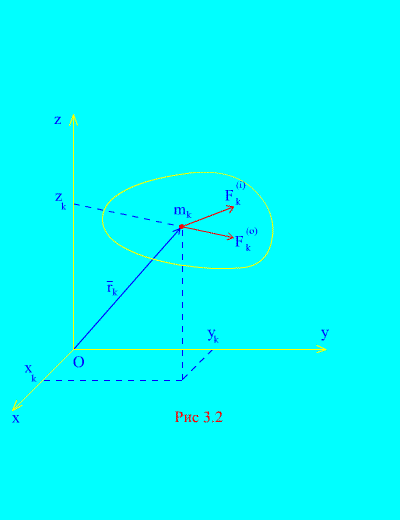
Пусть заданы внешние и внутренние силы, действующие на механическую систему, состоящую из N точек (рис. 3.2) . Если к каждой точке системы приложить равнодействующую внешних сил и равнодействующую всех внутренних сил , то для любой k -й точки системы можно составить дифференциальные уравнения движения. Всего таких уравнений будет N :

а в проекциях на неподвижные оси координат 3 N :

(3.4)

Векторные уравнения (3.3) или эквивалентные им скалярные уравнения (3.4) представляют дифференциальные законы движения материальных точек всей системы. Если все точки движутся параллельно одной плоскости или одной прямой, то число уравнений (3.4) в первом случае будет 2 N , во втором N .

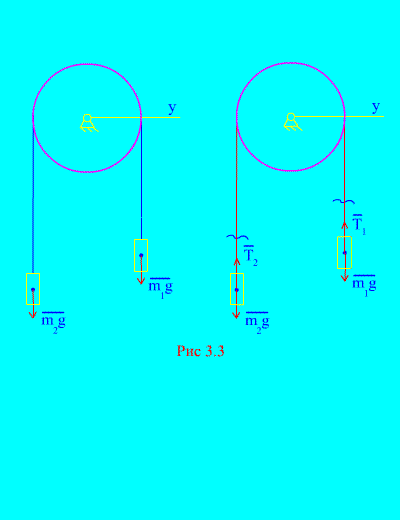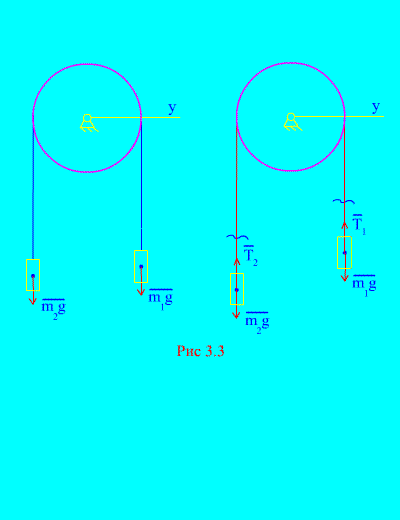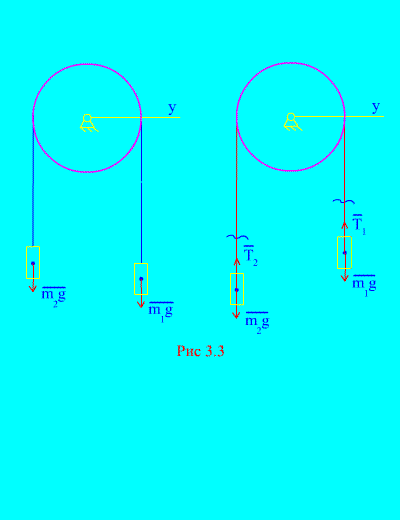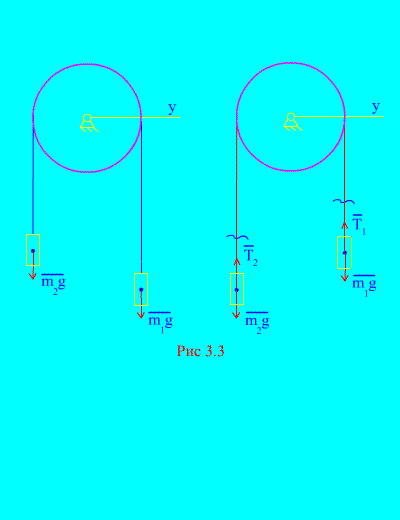
Пример 1. Два груза массой и связаны между собой нерастяжимым тросом, перекинутым через блок (рис. 3.3) . Пренебрегая силами трения, а также массой блока и троса, определить закон движения грузов и натяжения троса.

Решение . Система состоит из двух материальных тел (связанных нерастяжимым тросом), движущихся параллельно одной оси х. Запишем дифференциальные законы движения в проекциях на ось х для каждого тела.

Пусть правый груз опускается с ускорением , тогда левый груз будет подниматься с ускорением . Мысленно освобождаемся от связи (троса) и заменяем ее реакциями и (рис. 3.3) . Считая тела свободными, составим дифференциальные законы движения в проекции на ось х (имеется в виду, что натяжения нити являются внутренними силами, а вес грузов – внешними):

Поскольку и (тела связаны нерастяжимым тросом), получаем

Решая эти уравнения относительно ускорения и натяжения троса Т , получим

.

Отметим, что натяжение троса при не равно силе тяжести соответствующего груза.

3. 2. Теорема о движении центра масс

Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его.

Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.

Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде:

(3.5)

где N – число точек системы.

Сложим почленно уравнения между собой:

(а)

Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): где М – масса системы. Тогда левая часть равенства (а) запишется

Первая сумма, стоящая в правой части равенства (а), равна главному вектору внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется

, (3.6)

т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.

Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.

Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и L (рис. 3.4) .

Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом , длиной R + r в точке С 2 . Кривошип вращается с постоянной

угловой скоростью . В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.

Решение . Система состоит из двух масс (N =2 ): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.

Запишем теорему о движении центра масс (3.6) в координатной форме

Внешними силами этой системы являются: вес станины и неподвижного диска – Mg , вес подвижного диска – mg , - суммарная горизонтальная реакция болтов, - нормальная суммарная реакция плоскости. Следовательно,

Тогда законы движения (б) перепишутся

Вычислим координаты центра масс механической системы:

; (г)

как видно из (рис. 3.4) , , , (угол поворота кривошипа ), . Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от , , получим, что

(д)

Подставляя (в) и (д) в (б), находим

Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos = 1 соответственно, т.е

Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sin соответственно, т.е.

Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.

В условиях отсутствия брусков K и L (рис. 3.4) , механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда , т.е. когда , отсюда следует, что угловая скорость вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству

.

3. 3. Закон сохранения движения центра масс

Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. , то из (3.6) следует, что ускорение центра масс равно нулю, следовательно, скорость центра масс является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.

Из этой теоремы вытекает несколько следствий.

· Одними внутренними силами нельзя изменить характер движения центра масс системы.

· Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.

· Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.

· Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).

Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.

Пример 3. Два груза массами и соединены нерастяжимой нитью, переброшенной через блок (рис. 3.5) , закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.

Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести , и Mg , а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,

Поскольку в начальный момент система находилась в покое, имеем .

Вычислим координату центра масс системы при и в момент t 1 , когда груз весом g опустится на высоту H .

Для момента :

,

где , , х – соответственно координаты центра масс грузов весом g, g и клина весом М g .

Предположим, что клин в момент времени переместится в положительном направлении оси Ox на величину L , если груз весом опустится на высоту Н. Тогда, для момента

т.к. грузы вместе с клином передвинутся на L вправо, a груз переместится на расстояние по клину вверх. Так как , то после вычислений получим

.

3.4. Количество движения системы

3.4.1. Вычисление количества движения системы

Количеством движения материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости

Единица измерения количества движения -

Количеством движения механической системы называют векторную сумму количества движения отдельных точек системы, т.е.

где N – число точек системы.

Количество движения механической системы можно выразить через массу системы М и скорость центра масс . Действительно,

т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Направление совпадает с направлением (рис. 3.6)

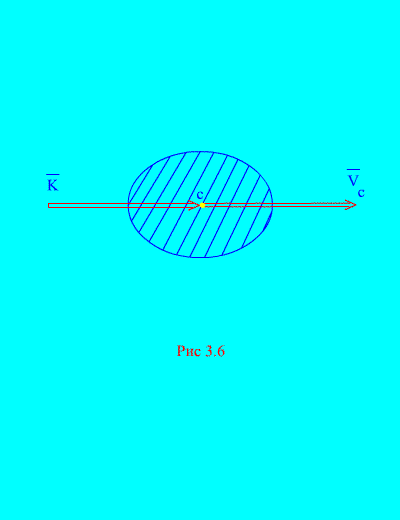
В проекциях на прямоугольные оси имеем

где , , - проекции скорости центра масс системы.

Здесь М – масса механической системы; не меняется при движении системы.

Этими результатами особенно удобно пользоваться при вычислении количеств движения твердых тел.

Из формулы (3.7) видно, что если механическая система движется так, что ее центр масс остается неподвижным, то количество движения системы остается равным нулю.

3.4.2. Элементарный и полный импульс силы

Действие силы на материальную точку в течение времени dt можно охарактеризовать элементарным импульсом . Полный импульс силы за время t , или импульс силы , определяют по формуле

или в проекциях на координаты оси

(3.8а)

Единица импульса силы - .

3.4.3. Теорема об изменении количества движения системы

Пусть к точкам системы приложены внешние и внутренние силы. Тогда для каждой точки системы можно применить дифференциальные законы движения (3.3), имея в виду, что :

.

Суммируя по всем точкам системы, получим

По свойству внутренних сил и по определению имеем

(3.9)

Умножая обе части этого уравнения на dt , получим теорему об изменении количества движения в дифференциальной форме:

, (3.10)

т.е. дифференциал количества движения механической системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на точки механической системы.

Вычисляя интеграл от обеих частей (3.10) по времени от 0 до t , получим теорему в конечной или интегральной форме

(3.11)

В проекциях на координатные оси будем иметь

Изменение количества движения механической системы за время t , равно векторной сумме всех импульсов внешних сил, действующих на точки механической системы за то же время.

Пример 4. Груз массой m спускается вниз по наклонной плоскости из состояния покоя под действием силы F , пропорциональной времени: , где (рис. 3.7) . Какую скорость приобретет тело через t секунд после начала движения, если коэффициент трения скольжения груза о наклонную плоскость равен f .

Решение. Изобразим силы, приложенные к грузу: mg – сила тяжести груза, N – нормальная реакция плоскости, - сила трения скольжения груза о плоскость, причем . Направление всех сил изображено на (рис. 3.7) .

Направим ось х вдоль наклонной плоскости вниз. Запишем теорему об изменении количества движения (3.11) в проекции на ось х :

(а)

По условию , т.к. в начальный момент времени груз находился в состоянии покоя. Сумма проекций импульсов всех сил на ось х равна

Следовательно,

,

.

3.4.4. Законы сохранения количества движения

Законы сохранения получаются как частные случаи теоремы об изменении количества движения. Возможны два частных случая.

· Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т.е. , то из теоремы следует (3.9) , что ,

т.е. если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению.

· Если проекция главного вектора внешних сил на какую-либо координатную ось равна нулю, например Ох, т.е. , то проекция количества движения на эту ось величина постоянная .

Рассмотрим пример применения закона сохранения количества движения.

Пример 5. Баллистический маятник представляет собой тело массой , подвешенное на длинной нити (рис. 3.8) .

Пуля массой , движущаяся со скоростью V и попадающая в неподвижное тело, застревает в нем, и тело отклоняется. Какова была скорость пули, если тело поднялось на высоту h ?

Решение. Пусть тело с застрявшей пулей приобрело скорость . Тогда, пользуясь законом сохранения количества движения при взаимодействии двух тел, можно записать .

Скорость можно вычислить, воспользовавшись законом сохранения механической энергии . Тогда . В результате находим

.

Пример 6 . Вода входит в неподвижный канал (рис. 3.9) переменного сечения со скоростью под углом к горизонту; площадь поперечного сечения канала при входе ; скорость воды у выхода из канала и составляет угол с горизонтом.

Определить горизонтальную составляющую реакции, которую вода оказывает на стенки канала. Плотность воды .

Решение. Будем определять горизонтальную составляющую реакции, оказываемой стенками канала на воду. Эта сила равна по модулю и противоположна по знаку искомой силе. Имеем, согласно (3.11а),

. (а)

Вычисляем массу объема жидкости, поступающей в канал за время t:

Величина rАV 0 называется секундной массой - масса жидкости, протекающей через любое сечение трубы в единицу времени.

Такое же количество воды покидает канал за это же время. Начальная и конечная скорости даны в условии.

Вычислим правую часть равенства (а) которая определяет сумму проекций на горизонтальную ось внешних сил, приложенных к системе (воде). Единственной горизонтальной силой является горизонтальная составляющая равнодействующей реакции стенок R x . Эта сила при установившемся движении воды является постоянной. Поэтому

. (в)

Подставляя (б) и (в) в (а), получаем

3.5. Кинетический момент системы

3.5.1. Главный момент количества движения системы

Пусть - радиус-вектор точки массой системы относительно некоторой точки А, называемой центром (рис. 3.10) .

Моментом количества движения (кинетическим моментом) точки относительно центра А называется вектор , определяемый по формуле

. (3.12)

При этом вектор направлен перпендикулярно плоскости, проходящей через центр А и вектор .

Моментом количества движения (кинетическим моментом) точки относительно оси называется проекция на эту ось момента количества движения точки относительно любого выбранного на данной оси центра.

Главным моментом количества движения (кинетическим моментом) системы относительно центра А называется величина

(3.13)

Главным моментом количества движения (кинетическим моментом) системы относительно оси называется проекция на эту ось главного момента количества движения системы относительно любого выбранного на данной оси центра.

3.5.2. Кинетический момент вращающегося твердого тела относительно оси вращения

Совместим неподвижную точку О тела, лежащую на оси вращения О z , с началом системы координат Оху z , оси которой будут вращаться вместе с телом (рис. 3.11) . Пусть - радиус-вектор точки тела относительно начала координат, его проекции на оси обозначим , , . Проекции вектора угловой скорости тела на те же оси обозначим 0, 0, ().

Здравствуйте! Меня зовут Александр Георгиевич и я являюсь московским профессиональным репетитором по информатике и программированию. Вам попалась задача, связанная с кодированием и , и вы запутались в алгоритме ее решения? Вам срочно нужно познакомиться с условием Фано , а также записаться ко мне на индивидуальные уроки. На своих уроках я акцентирую внимание на решении тематических простых и сложных упражнений.

В чем смысл прямого условия Фано?

Условие Фано названо в честь его создателя, итальянско-американского ученого Роберта Фано. Условие является необходимым в теории кодирования при построении самотерминирующегося кода. Учитывая другую терминологию, такой код называется префиксным.

Сформулировать данное условие можно следующим образом: «ни одно кодовое слово не может выступать в качестве начала любого другого кодового слова ».

С математической точки зрения условие можно сформулировать следующим образом: «если код содержит слово B, то для любой непустой строки C слова BC не существует в коде ».

В чем смысл обратного условия Фано?

Существует также и обратное правило Фано, формулировка которого звучит следующим образом: «ни одно кодовое слово не может выступать в качестве окончания любого другого кодового слова ».

С математической точки зрения обратное условие можно сформулировать следующим образом: «если код содержит слово B, то для любой непустой строки C слова CB не существует в коде ».

Практическое применение условия Фано

Рассмотрим телефонные номера в традиционной телефонии. Если уже существует номер «102», то номер «1029876» попросту не будет выдан. В случае набора первых трех цифр АТС перестает распознавать и принимать все остальные цифры, соединяя с абонентом по номеру 102. Однако это правило не является действительным для операторов мобильной связи. Связано это с тем, что для набора номера необходимо нажатие соответствующей клавиши, которой, в основном, является клавиша с изображением зеленой телефонной трубки. По этой причине, номера «102», «1020» и «1029876» могут существовать и быть закрепленными за разными адресатами.

Условие задачи: дана последовательность, которая состоит из букв «A», «B», «C», «D» и «E». Для кодирования приведенной последовательности применяется неравномерный двоичный код, при помощи которого можно осуществить однозначное декодирование.

Вопрос : есть ли возможность для одного из символов сократить длину кодового слова таким образом, чтобы сохранить возможность однозначного декодирования? При этом коды остальных символов должны остаться неизменными.

Решение : для того, чтобы сохранилась возможность декодирования, достаточным является соблюдение прямого или обратного условия Фано . Проведем последовательную проверку вариантов 1, 3 и 4. В случае если ни один из вариантов не подойдет, правильным ответом будет вариант 2 (не представляется возможным).

Вариант 1. Код: A - 00, B - 01, C - 011, D - 101, и E - 111. Прямое условие Фано не выполняется: код символа «B» совпадает с началом кода символа «C». Обратное правило Фано не выполняется: код символа «B» совпадает с окончанием кода символа «D». Вариант не является подходящим.

Вариант 3. Код: A - 00, B - 010, C - 01, D - 101, и E - 111. Прямое условие Фано не выполняется: код символа «C» совпадает с началом кода символа «B». Обратное условие также не выполняется: код символа «C» совпадает с окончанием кода символа «D». Вариант не является подходящим.

Вариант 4. Код: A - 00, B - 010, C - 011, D - 01, и E - 111. Прямое условие Фано не выполняется: код символа «D» совпадает с началом кода символов «B» и «C». Однако наблюдается выполнение обратного правила Фано: код символа «D» не совпадает с окончанием кода всех остальных символов. По этой причине, вариант является подходящим.

После проверки вариантов решения задачи на соответствие прямому и обратному условию Фано , было установлено, что правильным является вариант 4.

Ответ : 4

А сейчас я вам предлагаю ознакомиться с мультимедийным решением задачи, которая была предложена в демонстрационном варианте ЕГЭ по информатике и ИКТ. Кстати, данная задача относится к типу задач, решаемых с использованием условия Фано .

Остались вопросы?

Если после прочтения данной публикации у вас все равно остались какие-то вопросы, непонимания или вы хотите закрепить пройденный материал практическими решениями, то звоните и записывайтесь ко мне на частные уроки по информатике и ИКТ.

Задание 31. Неравномерные коды. Условие Фано

5-54.Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г использовали такие кодовые слова: А - 001, Б - 010, В - 000, Г - 011.

Укажите, каким кодовым словом из перечисленных ниже может быть закодирована буква Д.

Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

1) 00 2) 01 3) 0000 4) 101

5-85. Для кодирования некоторой последовательности, состоящей из букв У, Ч, Е, Н, И и К, используется неравномерный двоичный префиксный код. Вот этот код: У – 000, Ч – 001, Е – 010, Н – 100, И – 011, К – 11. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему остался префиксным? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.

Примечание. Префиксный код – это код, в котором ни одно кодовое слово не является началом другого; такие коды позволяют однозначно декодировать полученную двоичную последовательность.

1) кодовое слово для буквы Е можно сократить до 01

2) кодовое слово для буквы К можно сократить до 1

3) кодовое слово для буквы Н можно сократить до 10

4) это невозможно

5-94. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 1, для буквы Б – кодовое слово 011. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?

5-74. По каналу связи передаются сообщения, содержащие только 4 буквы: E, Н, О, Т. В любом сообщении больше всего букв О, следующая по частоте буква – Е, затем – Н. Буква Т встречается реже, чем любая другая. Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?

1) Е – 0, Н – 1, О – 00, Т – 11 2) О – 1, Н – 0, Е – 01, Т – 10

3) Е – 1, Н – 01, О – 001, Т – 000 4) О – 0, Н – 10, Е – 111, Т – 110

5-105. По каналу связи передаются сообщения, каждое из которых содержит 15 букв А, 10 букв Б, 6 букв В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:

а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);

б) общая длина закодированного сообщения должна быть как можно меньше.

Какой код из приведённых ниже следует выбрать для кодирования букв А, Б, В и Г?

1) А:1, Б:01, В:001, Г:111

2) А:1, Б:01, В:10, Г:111

3) А:00, Б:01, В:10, Г:11

4) А:100, Б:101, В:11, Г:0

5-102. В сообщении встречается 10 разных букв. При его передаче использован неравномерный двоичный префиксный код. Известны коды трех букв: 11, 100, 101. Коды остальных семи букв имеют одинаковую длину. Какова минимальная суммарная длина всех 10-ти кодовых слов?

5-104. В сообщении встречается 50 букв А, 30 букв Б, 20 букв В и 5 букв Г. При его передаче использован неравномерный двоичный префиксный код, который позволил получить минимальную длину закодированного сообщения. Какова она в битах?

По каналу связи передаются сообщения, содержащие только пять букв: A, B, С, D, E. Для передачи используется двоичный код, допускающий однозначное декодирование. Для буквA, B, C используются такие кодовые слова: A – 111, B – 0, C – 100.

Укажите кратчайшее кодовое слово для буквыD, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

9-1-23. После преобразования растрового 256-цветного графического файла в 16-цветный формат его размер уменьшился на 15 Кбайт. Каков был размер исходного файла в Кбайтах?

9-1-25. После преобразования растрового графического файла его объем уменьшился в 1,5 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 16-цветной палитре?

13-37. При регистрации в компьютерной системе каждому пользователю выдаётся идентификатор, состоящий из 8 символов, первый и последний из которых – одна из 18 букв, а остальные – цифры (допускается использование 10 десятичных цифр). Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти в байтах, отводимый этой программой для записи 500 паролей.

13-38. При регистрации в компьютерной системе, используемой при проведении командной олимпиады, каждому ученику выдается уникальный идентификатор – целое число от 1 до 1000. Для хранения каждого идентификатора используется одинаковое и минимально возможное количество бит. Идентификатор команды состоит из последовательно записанных идентификаторов учеников и 8 дополнительных бит. Для записи каждого идентификатора команды система использует одинаковое и минимально возможное количество байт. Во всех командах равное количество участников. Сколько участников в каждой команде, если для хранения идентификаторов 20 команд-участниц потребовалось 180 байт?

13-50. При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, K, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей. Для хранения сведений о 20 пользователях потребовалось 300 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число – количество байт.

16-165. Значение арифметического выражения: 9 22 + 3 66 – 18 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?