პროექციის მატრიცა. ზოგადი პერსპექტივის ტრანსფორმაციის მატრიცა. სრული პერსპექტივის პროექციის მოდელი

17.04.2019

ძრავა ხომალდს არ მოძრაობს. გემი თავის ადგილზე რჩება და ძრავა სამყაროს მის მიმართ მოძრაობს.

ეს ძალიან მნიშვნელოვანი ნაწილიგაკვეთილები, დარწმუნდით, რომ რამდენჯერმე წაიკითხეთ და კარგად გესმით.

ერთგვაროვანი კოორდინატები

მანამდე მიმდინარე მომენტიჩვენ ვიმოქმედეთ 3-განზომილებიან წვეროებზე, როგორც (x, y, z) სამეულები. შემოვიღოთ სხვა პარამეტრი w და ვიმოქმედოთ ფორმის ვექტორებით (x, y, z, w).

დაიმახსოვრე სამუდამოდ, რომ:

თუ w == 1, მაშინ ვექტორი (x, y, z, 1) არის პოზიცია სივრცეში.
თუ w == 0, მაშინ ვექტორი (x, y, z, 0) არის მიმართულება.

რას გვაძლევს ეს? კარგი, ბრუნვისთვის ეს არაფერს ცვლის, რადგან წერტილის ბრუნვის შემთხვევაშიც და მიმართულების ვექტორის ბრუნვის შემთხვევაშიც იგივე შედეგს მიიღებთ. თუმცა გადაცემის შემთხვევაში არის განსხვავება. მიმართულების ვექტორის თარგმნა იგივე ვექტორს მისცემს. ამაზე დაწვრილებით მოგვიანებით ვისაუბრებთ.

ერთგვაროვანი კოორდინატები გვაძლევს საშუალებას, ერთის გამოყენებით მათემატიკური ფორმულავექტორებით მუშაობა ორივე შემთხვევაში.

ტრანსფორმაციის მატრიცები

შესავალი მატრიცებში

მატრიცის წარმოდგენის უმარტივესი გზა არის რიცხვების მასივი, მკაცრად გარკვეული თანხარიგები და სვეტები. მაგალითად, 2x3 მატრიცა ასე გამოიყურება:

თუმცა, in 3D გრაფიკაჩვენ გამოვიყენებთ მხოლოდ 4x4 მატრიცებს, რომლებიც საშუალებას მოგვცემს გარდაქმნას ჩვენი წვეროები (x, y, z, w). გარდაქმნილი წვერო არის მატრიცის გამრავლების შედეგი თავად წვეროზე:

Matrix x Vertex (ამ თანმიმდევრობით!!) = ტრანსფორმაცია. წვერო

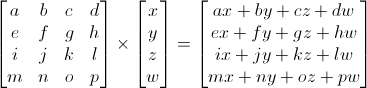
Საკმაოდ მარტივი. ჩვენ ამას საკმაოდ ხშირად გამოვიყენებთ, ამიტომ აზრი აქვს კომპიუტერს ამის გაკეთება:

C++-ში, GLM-ის გამოყენებით:

glm::mat4 myMatrix; glm::vec4 myVector; გლმ:: // შეკვეთას მიაქციე ყურადღება! ის მნიშვნელოვანია!

GLSL-ში:

mat4 myMatrix; vec4 myVector ; // არ დაგავიწყდეთ მატრიცის და ვექტორის შევსება საჭირო მნიშვნელობებით vec4 transformedVector = myMatrix * myVector ; // დიახ, ის ძალიან ჰგავს GLM-ს :)

სცადეთ ექსპერიმენტები ამ ფრაგმენტებით.

გადაცემის მატრიცა

გადაცემის მატრიცა ასე გამოიყურება:

სადაც X, Y, Z არის მნიშვნელობები, რომლებიც გვინდა დავამატოთ ჩვენს ვექტორს.

ასე რომ, თუ გვსურს ვექტორი (10, 10, 10, 1) გადავიტანოთ 10 ერთეულით X მიმართულებით, მივიღებთ:

... ვიღებთ (20, 10, 10, 1) ერთგვაროვან ვექტორს! გახსოვდეთ, რომ w პარამეტრში 1 ნიშნავს პოზიციას და არა მიმართულებას და ჩვენმა ტრანსფორმაციამ არ შეცვალა ის ფაქტი, რომ ჩვენ ვმუშაობთ პოზიციაზე.

ახლა ვნახოთ რა მოხდება, თუ ვექტორი (0, 0, -1, 0) წარმოადგენს მიმართულებას:

... და მივიღებთ ჩვენს თავდაპირველ ვექტორს (0, 0, -1, 0). როგორც უკვე აღვნიშნეთ, პარამეტრის w = 0 ვექტორის გადატანა შეუძლებელია.

ახლა დროა ჩაწეროთ ის კოდში.

C++-ში, GLM-ით:

#შეიცავს // შემდეგ glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0 f, 0.0 f, 0.0 f)); glm::vec4 myVector(10.0 f, 10.0 f, 10.0 f, 0.0 f); glm::vec4 transformedVector = myMatrix * myVector ;

GLSL-ში:

vec4 transformedVector = myMatrix * myVector ;

სინამდვილეში, თქვენ არასოდეს გააკეთებთ ამას shader-ში, ყველაზე ხშირად გააკეთებთ glm::translate()-ში C++-ში მატრიცის გამოსათვლელად, გადასცემთ მას GLSL-ზე და შემდეგ შეასრულებთ გამრავლებას შადერში.

იდენტობის მატრიცა

ეს სპეციალური მატრიცა, რომელიც არაფერს აკეთებს, მაგრამ ჩვენ მას ვეხებით, რადგან მნიშვნელოვანია გვახსოვდეს, რომ A გამრავლებული 1.0-ზე იძლევა A:

C++-ში:

glm::mat4 myIdentityMatrix = glm::mat4(1.0 f);

სკალირების მატრიცა

ის ისევე მარტივად გამოიყურება:

ასე რომ, თუ გსურთ გამოიყენოთ ვექტორული სკალირება (პოზიცია ან მიმართულება - არ აქვს მნიშვნელობა) 2.0-ით ყველა მიმართულებით, მაშინ გჭირდებათ:

გაითვალისწინეთ, რომ w არ იცვლება და ასევე გაითვალისწინეთ, რომ პირადობის მატრიცა- ეს განსაკუთრებული შემთხვევასკალირების მატრიცები მასშტაბის კოეფიციენტით 1-ის ტოლი ყველა ღერძზე. ასევე, იდენტურობის მატრიცა არის გადაცემის მატრიცის განსაკუთრებული შემთხვევა, სადაც (X, Y, Z) = (0, 0, 0), შესაბამისად.

C++-ში:

// დაამატეთ #include და # მოიცავს glm::mat4 myScalingMatrix = glm::scale(2.0 f, 2.0 f, 2.0 f);

ბრუნვის მატრიცა

უფრო რთული, ვიდრე ადრე განვიხილეთ. ჩვენ გამოვტოვებთ დეტალებს აქ, რადგან თქვენ არ გჭირდებათ ამის ზუსტად ცოდნა ყოველდღიური გამოყენებისთვის. მეტის მისაღებად დეტალური ინფორმაციაშეგიძლიათ მიჰყვეთ ბმულს Matrices and Quaternions FAQ (საკმაოდ პოპულარული რესურსია და თქვენი ენა შეიძლება იქ იყოს ხელმისაწვდომი)

C++-ში:

// დაამატეთ #include და # მოიცავს glm::vec3 myRotationAxis ( ?? , ?? , ?? ); glm::rotate(კუთხე_ში_გრადუსებში, myRotationAxis);

გარდაქმნების გაერთიანება

ახლა ჩვენ შეგვიძლია დავატრიალოთ, გადავთარგმნოთ და გავაფართოვოთ ჩვენი ვექტორები. შემდეგი ნაბიჯი იქნება გარდაქმნების გაერთიანება, რომელიც ხორციელდება შემდეგი ფორმულის გამოყენებით:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector ;

ყურადღება! ეს ფორმულა რეალურად აჩვენებს, რომ ჯერ კეთდება სკალირება, შემდეგ კეთდება როტაცია და მხოლოდ მაქსიმუმამდე ბოლო საშუალებატრანსფერი მიმდინარეობს. ზუსტად ასე მუშაობს მატრიცული გამრავლება.

დარწმუნდით, რომ დაიმახსოვრეთ რა თანმიმდევრობით კეთდება ეს ყველაფერი, რადგან თანმიმდევრობა ნამდვილად მნიშვნელოვანია, ბოლოს და ბოლოს, შეგიძლიათ თავად შეამოწმოთ:

გადადგი ნაბიჯი წინ და მოუხვიე მარცხნივ
მოუხვიეთ მარცხნივ და გადადგი ნაბიჯი წინ

განსხვავების გაგება ნამდვილად მნიშვნელოვანია, რადგან ამას ყოველთვის შეხვდებით. მაგალითად, როდესაც თქვენ მუშაობთ თამაშის პერსონაჟებთან ან ზოგიერთ ობიექტთან, ყოველთვის ჯერ გააფართოვეთ, შემდეგ გადაატრიალეთ და მხოლოდ ამის შემდეგ გადათარგმნეთ.

ფაქტობრივად, ზემოაღნიშნული თანმიმდევრობა არის ის, რაც ზოგადად გჭირდებათ თამაშის პერსონაჟებისთვის და სხვა ნივთებისთვის: საჭიროების შემთხვევაში, ჯერ გააფართოვეთ იგი; შემდეგ დააყენეთ მისი მიმართულება და შემდეგ გადაიტანეთ იგი. მაგალითად, გემის მოდელისთვის (როტაციები ამოღებულია სიმარტივისთვის):

Არასწორი გზა:
- თქვენ გადაიტანეთ გემი (10, 0, 0). მისი ცენტრი ახლა წარმოშობიდან 10 ერთეულია.
- თქვენ ადიდებთ თქვენს გემს 2-ჯერ. თითოეული კოორდინატი მრავლდება 2-ზე „ორიგინთან შედარებით“, რაც შორს არის... ასე რომ, თქვენ აღმოჩნდებით დიდ გემში, მაგრამ მისი ცენტრი არის 2 * 10 = 20. არა ის, რაც გინდოდათ.
სწორი გზა:
- თქვენ ადიდებთ თქვენს გემს 2-ჯერ. თქვენ მიიღებთ დიდ გემს, რომელიც ორიენტირებულია საწყისზე.
- თქვენ გადაადგილდებით თქვენს გემს. ის მაინც იგივე ზომისაა და სწორ მანძილზეა.

C++-ში, GLM-ით:

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix ; glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

GLSL-ში:

mat4 ტრანსფორმაცია = mat2 * mat1 ; vec4 out_vec = გარდაქმნა * in_vec ;

სამყარო, ხედვა და პროექციის მატრიცები

ამ გაკვეთილის დანარჩენი ნაწილისთვის, ჩვენ ვივარაუდებთ, რომ ვიცით როგორ გამოვიტანოთ ბლენდერის საყვარელი 3D მოდელი, Suzanne the Monkey.

სამყარო, ხედვა და პროექციის მატრიცები არის მოსახერხებელი ინსტრუმენტიგარდაქმნების გამოყოფა.

მსოფლიო მატრიცა

ეს მოდელი, ისევე როგორც ჩვენი წითელი სამკუთხედი, განისაზღვრება წვეროების სიმრავლით, რომელთა კოორდინატები მოცემულია ობიექტის ცენტრთან მიმართებაში, ანუ წვერო კოორდინატებით (0, 0, 0) იქნება ცენტრში. ობიექტი.

შემდეგ ჩვენ გვინდა გადავიტანოთ ჩვენი მოდელი, რადგან მოთამაშე აკონტროლებს მას კლავიატურისა და მაუსის გამოყენებით. ჩვენ მხოლოდ ვიყენებთ სკალირებას, შემდეგ ვატრიალებთ და ვთარგმნით. ეს მოქმედებები შესრულებულია თითოეული წვეროსთვის, თითოეულ ჩარჩოში (შესრულებულია GLSL-ში და არა C++-ში!) და ამით ჩვენი მოდელი მოძრაობს ეკრანზე.

ახლა ჩვენი მწვერვალები მსოფლიო სივრცეში. ეს ნაჩვენებია ნახატზე შავი ისრით. ჩვენ გადავედით ობიექტის სივრციდან (ყველა წვერო განისაზღვრება ობიექტის ცენტრთან მიმართებით) მსოფლიო სივრცეში (ყველა წვერო განისაზღვრება სამყაროს ცენტრთან მიმართებაში).

ეს სქემატურად ასეა ნაჩვენები:

მატრიცის ნახვა

კიდევ ერთხელ მოვიყვანოთ ფუტურამას ციტატა:

ძრავა ხომალდს არ მოძრაობს. გემი რჩება იმავე ადგილას და ძრავა მოძრაობს სამყაროს მის გარშემო.

შეეცადეთ წარმოიდგინოთ ეს კამერასთან მიმართებაში. მაგალითად, თუ გსურს მთის ფოტოს გადაღება, კამერას კი არ ამოძრავებ, არამედ მთას. ეს შეუძლებელია შიგნით ნამდვილი ცხოვრება, მაგრამ ეს წარმოუდგენლად ადვილია კომპიუტერული გრაფიკა.

ასე რომ, თავდაპირველად თქვენი კამერა მსოფლიო კოორდინატთა სისტემის ცენტრშია. სამყაროს გადასატანად თქვენ უნდა შეიყვანოთ სხვა მატრიცა. ვთქვათ, გსურთ გადაიტანოთ კამერა 3 ერთეულით მარჯვნივ (+X), რაც მთელი სამყაროს 3 ერთეულით მარცხნივ (-X) გადაადგილების ტოლფასია. კოდში ასე გამოიყურება:

// დაამატეთ #include და # მოიცავს glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0 f, 0.0 f, 0.0 f));

კიდევ ერთხელ, ქვემოთ მოყვანილი სურათი სრულად აჩვენებს ამას. ჩვენ გადავედით მსოფლიო კოორდინატთა სისტემიდან (ყველა წვერო დაყენებულია მსოფლიო სისტემის ცენტრთან მიმართებაში) კამერის კოორდინატულ სისტემაში (ყველა წვერო დაყენებულია კამერის მიმართ):

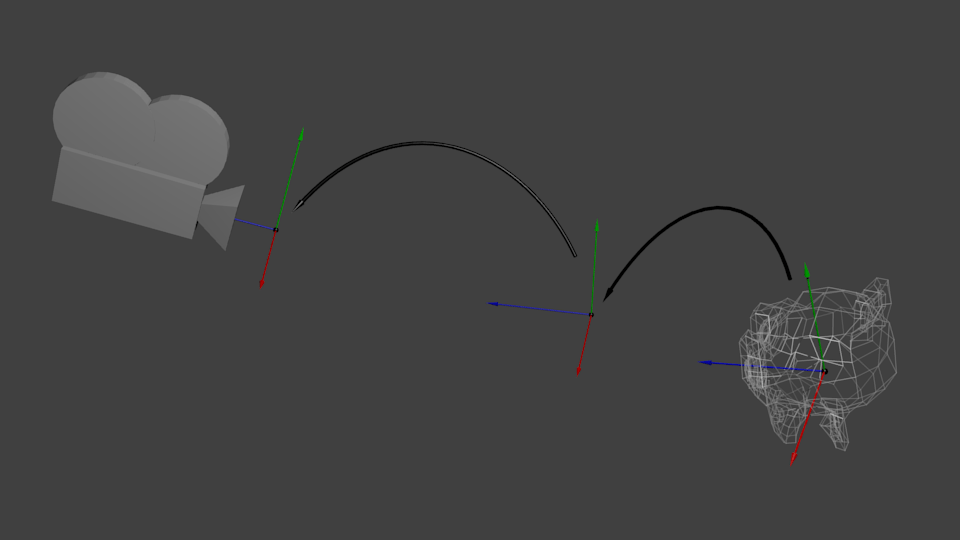
და სანამ თქვენი ტვინი ამას ითვისებს, ჩვენ გადავხედავთ იმ ფუნქციას, რომელსაც GLM გვაწვდის, უფრო კონკრეტულად glm::LookAt:

glm::mat4 CameraMatrix = glm::LookAt(კამერის პოზიცია, // კამერის პოზიცია მსოფლიო სივრცეში cameraTarget // მიუთითებს სად იყურებით მსოფლიო სივრცეში upVector // აღმავალი მიმართულების აღმნიშვნელი ვექტორი. როგორც წესი (0, 1, 0));

და აქ არის დიაგრამა, რომელიც აჩვენებს რას ვაკეთებთ:

თუმცა, ეს არ არის დასასრული.

პროექციის მატრიცა

ასე რომ, ახლა ჩვენ კამერის სივრცეში ვართ. ეს ნიშნავს, რომ წვერო, რომელიც იღებს კოორდინატებს x == 0 და y == 0, გამოჩნდება ეკრანის ცენტრში. თუმცა ობიექტის ჩვენებისას დიდ როლს თამაშობს მანძილი კამერამდე (z). ორი წვეროსთვის, რომლებსაც აქვთ იგივე x და y, უფრო დიდი z მნიშვნელობის მქონე წვერო გამოჩნდება უფრო ახლოს, ვიდრე მეორე.

ამას ჰქვია პერსპექტიული პროექცია:

და ჩვენთვის საბედნიეროდ, 4x4 მატრიცას შეუძლია გააკეთოს ეს პროექცია:

// ქმნის მართლაც რთულად წასაკითხ მატრიცას, მაგრამ ის მაინც სტანდარტული 4x4 მატრიცაა glm::mat4 projectionMatrix = glm::პერსპექტივა (glm::რადიანი (FoV), // ვერტიკალური ხედვის ველი რადიანებში. როგორც წესი, 90° (ძალიან ფართო) და 30° (ვიწრო) შორის 4.0 f/3.0 f // ასპექტის თანაფარდობა. დამოკიდებულია თქვენი ფანჯრის ზომაზე. გაითვალისწინეთ, რომ 4/3 == 800/600 == 1280/960 0.1 ფ // საჭრელი თვითმფრინავის მახლობლად. 0-ზე მეტი უნდა იყოს. 100.0f // შორს ჭრის თვითმფრინავი.);

ჩვენ გადავედით Camera Space-დან (ყველა წვერო განსაზღვრულია კამერის მიმართ) ჰომოგენურ სივრცეში (ყველა წვერო პატარა კუბშია. ეკრანზე ნაჩვენებია ყველაფერი, რაც კუბის შიგნით არის).

ახლა მოდით შევხედოთ შემდეგი სურათები, რათა უკეთ გაიგოთ რა ხდება პროექციასთან დაკავშირებით. პროექციამდე ჩვენ გვაქვს ლურჯი ობიექტები კამერის სივრცეში, ხოლო წითელი ფიგურა აჩვენებს კამერის ხედს, ანუ ყველაფერს, რასაც კამერა ხედავს.

პროექციის მატრიცის გამოყენება იძლევა შემდეგ ეფექტს:

ამ სურათზე კამერის ხედი არის კუბი და ყველა ობიექტი დეფორმირებულია. ობიექტები, რომლებიც უფრო ახლოს არიან კამერასთან, დიდი ჩანს, ხოლო უფრო შორს, პატარა. ისევე, როგორც სინამდვილეში!

ასე გამოიყურება:

გამოსახულება კვადრატულია, ამიტომ შემდეგი მათემატიკური გარდაქმნები გამოიყენება გამოსახულების მიხედვით გასაჭიმად მიმდინარე ზომებიფანჯარა:

და ეს სურათი არის ის, რაც რეალურად გამოვა.

ტრანსფორმაციების გაერთიანება: ModelViewProjection მატრიცა

... მხოლოდ სტანდარტული მატრიცის გარდაქმნები, რომლებიც უკვე გიყვართ!

// C++ : მატრიცის გაანგარიშება glm::mat4 MVPmatrix = პროექცია * ხედი * მოდელი ; // დაიმახსოვრე! IN საპირისპირო მიზნით!

// GLSL: გამოიყენეთ მატრიცა transformed_vertex = MVP * in_vertex ;

ყველაფერს ერთად ათავსებ

პირველი ნაბიჯი არის ჩვენი MVP მატრიცის შექმნა. ეს უნდა გაკეთდეს თითოეული მოდელისთვის, რომელსაც თქვენ აჩვენებთ.

// სროლის მატრიცა: 45° ხედვის ველი, 4:3 თანაფარდობა, დიაპაზონი: 0.1 ერთეული<->100 ერთეული glm::mat4 პროექცია = glm::პერსპექტივა(glm::radians(45.0 f), 4.0 f / 3.0 f, 0.1 f, 100.0 f); // ან, ორთოკამერისთვის glm::mat4 ხედი = glm::lookAt(glm::vec3(4, 3, 3), // კამერა არის მსოფლიო კოორდინატებში (4,3,3) glm::vec3(0, 0, 0), // და მიმართულია წარმოშობისაკენ glm::vec3(0, 1, 0) // "თავი" არის ზევით); // მოდელის მატრიცა: იდენტურობის მატრიცა (მოდელი სათავეშია) glm::mat4 მოდელი = glm::mat4(1.0 f); // ინდივიდუალურად თითოეული მოდელისთვის // საბოლოო ModelViewProjection მატრიცა, რომელიც არის ჩვენი სამი მატრიცის გამრავლების შედეგი glm::mat4 MVP = პროექცია * ხედი * მოდელი ; // გახსოვდეთ, რომ მატრიცის გამრავლება ხდება საპირისპირო თანმიმდევრობით

მეორე ნაბიჯი არის ამის გადაცემა GLSL-ზე:

// მიიღეთ ცვლადის სახელური შადერში // მხოლოდ ერთხელ ინიციალიზაციის დროს. GLuint MatrixID = glGetUniformLocation(პროგრამის ID, "MVP"); // გადავიტანოთ ჩვენი ტრანსფორმაციები მიმდინარე შადერზე // ეს კეთდება მთავარ ციკლში, ვინაიდან თითოეულ მოდელს ექნება განსხვავებული MVP მატრიცა (მინიმუმ ნაწილი M) glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);

მესამე ნაბიჯი არის მიღებული მონაცემების გამოყენება GLSL-ში ჩვენი წვეროების გარდაქმნისთვის.

// Vertex შეყვანის მონაცემები, განსხვავებულია ამ shader-ის ყველა შესრულებისთვის.განლაგება (ადგილმდებარეობა = 0) vec3 vertexPosition_modelspace-ში; // მნიშვნელობები, რომლებიც მუდმივი რჩება მთელი ქსელისთვის.ერთიანი mat4 MVP; ცარიელი მთავარი ()( // ჩვენი წვეროს გამომავალი პოზიცია: MVP * პოზიცია gl_Position = MVP * vec4 (vertexPosition_modelspace, 1); )

მზადაა! ახლა ჩვენ გვაქვს იგივე სამკუთხედი, როგორც მე-2 გაკვეთილში, რომელიც ჯერ კიდევ მდებარეობს საწყისზე (0, 0, 0), მაგრამ ახლა მას ვხედავთ პერსპექტივაში (4, 3, 3).

მე-6 გაკვეთილზე თქვენ შეისწავლით თუ როგორ შეცვალოთ ეს მნიშვნელობები დინამიურად თქვენი კლავიატურისა და მაუსის გამოყენებით, რათა შექმნათ კამერა, რომელსაც თამაშებში ხედავთ. მაგრამ პირველ რიგში, ჩვენ ვისწავლით, როგორ მივცეთ ჩვენს მოდელებს ფერები (გაკვეთილი 4) და ტექსტურები (გაკვეთილი 5).

Დავალებები

სცადეთ glm::perspective მნიშვნელობების შეცვლა
პერსპექტიული პროექციის გამოყენების ნაცვლად, სცადეთ გამოიყენოთ ორთოგონალური (glm:ortho)
შეცვალეთ ModelMatrix სამკუთხედის გადასატანად, დასატრიალებლად და მასშტაბირება
გამოიყენეთ წინა დავალება, მაგრამ თან სხვადასხვა თანმიმდევრობითოპერაციები. ყურადღება მიაქციეთ შედეგს.

გარკვეულ მომენტში, კომპიუტერული გრაფიკის დარგის ნებისმიერ დეველოპერს აქვს შეკითხვა: როგორ მუშაობს ეს პერსპექტიული მატრიცები? ზოგჯერ პასუხის პოვნა ძალიან რთულია და, როგორც ჩვეულებრივ ხდება, დეველოპერების უმეტესობა უარს ამბობს დავალების ნახევარზე.

ეს არ არის პრობლემის გადაწყვეტა! მოდით ერთად გავარკვიოთ!

ვიყოთ რეალისტები პრაქტიკული მიკერძოებით და მივიღოთ როგორც ტესტის საგანი OpenGL ვერსიები 3.3. ამ ვერსიიდან დაწყებული, თითოეული დეველოპერი ვალდებულია დამოუკიდებლად განახორციელოს მოდული მატრიცული ოპერაციები. კარგია, ეს არის ის, რაც ჩვენ გვჭირდება. მოდით დავშალოთ ჩვენი რთული ამოცანა და გამოვყოთ ძირითადი პუნქტები. ზოგიერთი ფაქტი OpenGL სპეციფიკაციიდან:

მატრიცები ინახება სვეტებში (სვეტი-ძირითადი);
ერთგვაროვანი კოორდინატები;
კანონიკური ამოკვეთის მოცულობა (CVV) მარცხენა კოორდინატულ სისტემაში.

მატრიცების შესანახად ორი გზა არსებობს: სვეტი-მაჟორი და მწკრივი-მაჟორი. წრფივი ალგებრაზე ლექციებში გამოიყენება მწკრივის ძირითადი სქემა. მიერ დიდწილადმეხსიერებაში მატრიცების წარმოდგენას მნიშვნელობა არ აქვს, რადგან მატრიცა ყოველთვის შეიძლება გადაიზარდოს ერთი წარმოდგენიდან მეორეზე მარტივი ტრანსპოზიციით. და რადგან განსხვავება არ არის, მაშინ ყველა შემდგომი გამოთვლებისთვის ჩვენ გამოვიყენებთ კლასიკურ მწკრივის ძირითად მატრიცებს. ზე OpenGL პროგრამირებაარსებობს პატარა ხრიკი, რომელიც საშუალებას გაძლევთ უარი თქვათ მატრიცების ტრანსპოზირებაზე კლასიკური მწკრივის ძირითადი გამოთვლების შენარჩუნებით. მატრიცა უნდა გადავიდეს შადერის პროგრამაში, როგორც არის, ხოლო ჩრდილში გამრავლება უნდა განხორციელდეს არა ვექტორსა და მატრიცას შორის, არამედ მატრიცასა და ვექტორს შორის.

ერთგვაროვანი კოორდინატები არც თუ ისე კარგია მზაკვრული სისტემაგვერდით მარტივი წესებიჩვეულებრივი დეკარტის კოორდინატების ერთგვაროვან კოორდინატებად გადაქცევაზე და პირიქით. ერთგვაროვანი კოორდინატი არის განზომილების მწკრივის მატრიცა. დეკარტის კოორდინატის ერთგვაროვან კოორდინატად გადაქცევისთვის აუცილებელია x, წდა ზგავამრავლოთ ნებისმიერზე ნამდვილი რიცხვი ვ(0-ის გარდა). შემდეგი, თქვენ უნდა ჩაწეროთ შედეგი პირველ სამ კომპონენტში, ხოლო ბოლო კომპონენტი ტოლი იქნება მულტიპლიკატორის ვ. Სხვა სიტყვებით:
- დეკარტის კოორდინატები
ვ- რეალური რიცხვი არ უდრის 0-ს

- ერთგვაროვანი კოორდინატები

პატარა ხრიკი: თუ ვუდრის ერთს, მაშინ თარგმანისთვის საჭიროა მხოლოდ კომპონენტების გადატანა x, წდა ზდა მივანიჭოთ ერთი ბოლო კომპონენტს. ანუ მიიღეთ მწკრივის მატრიცა:

რამდენიმე სიტყვა ნულოვანი ხარისხის შესახებ ვ. ერთგვაროვანი კოორდინატების თვალსაზრისით, ეს საკმაოდ მისაღებია. ერთგვაროვანი კოორდინატები საშუალებას გაძლევთ განასხვავოთ წერტილები და ვექტორები. დეკარტის კოორდინატულ სისტემაში ასეთი დაყოფა შეუძლებელია.

- წერტილი, სადაც ( x, y, z) – დეკარტის კოორდინატები

- ვექტორი, სადაც ( x, y, z) – რადიუსის ვექტორი

წვეროების საპირისპირო გადათარგმნა ერთგვაროვანი კოორდინატებიდან დეკარტის კოორდინატებზე ხორციელდება შემდეგნაირად. მწკრივის მატრიცის ყველა კომპონენტი უნდა დაიყოს ბოლო კომპონენტი. Სხვა სიტყვებით:

- ერთგვაროვანი კოორდინატები
- დეკარტის კოორდინატები

მთავარია, რაც თქვენ უნდა იცოდეთ არის ის, რომ OpenGL კლიპის და რასტერიზაციის ყველა ალგორითმი მუშაობს დეკარტის კოორდინატებში, მაგრამ მანამდე ყველა ტრანსფორმაცია ხორციელდება ერთგვაროვან კოორდინატებში. ჰომოგენური კოორდინატებიდან დეკარტის კოორდინატებზე გადასვლა ხორციელდება აპარატურაში.

კანონიკური ამოკვეთის მოცულობა (CVV) არის OpenGL-ის ერთ-ერთი ყველაზე ნაკლებად დოკუმენტირებული ნაწილი. როგორც ჩანს ნახ. 1 CVV არის ღერძზე გასწორებული კუბი, რომელიც ორიენტირებულია საწყისზე და კიდის სიგრძე უდრის ორს. ყველაფერი, რაც შედის CVV ზონაში, ექვემდებარება რასტერიზაციას, ყველაფერი, რაც არის CVV-ს გარეთ, იგნორირებულია. ყველაფერი, რაც ნაწილობრივ ცდება CVV-ს მიღმა, ექვემდებარება მორთვის ალგორითმებს. ყველაზე მნიშვნელოვანი რაც თქვენ უნდა იცოდეთ არის ის, რომ CVV კოორდინატთა სისტემა მემარცხენეა!

ბრინჯი. 1. კანონიკური OpenGL ამოკვეთის მოცულობა (CVV)

მარცხენა კოორდინატთა სისტემა? როგორ შეიძლება ეს იყოს, ვინაიდან OpenGL 1.0-ის სპეციფიკაცია ნათლად ამტკიცებს, რომ გამოყენებული კოორდინატთა სისტემა მემარჯვენეა? მოდი გავარკვიოთ.

ბრინჯი. 2. საკოორდინაციო სისტემები

როგორც ჩანს ნახ. 2 კოორდინატთა სისტემა განსხვავდება მხოლოდ ღერძის მიმართულებით ზ. OpenGL 1.0 რეალურად იყენებს მემარჯვენეებს მომხმარებლის სისტემაკოორდინატები მაგრამ CVV კოორდინატთა სისტემა და მომხმარებლის კოორდინატთა სისტემა ორი სრულიად განსხვავებული რამ არის. უფრო მეტიც, 3.3 ვერსიის მდგომარეობით, ასეთი რამ აღარ არსებობს სტანდარტული სისტემა OpenGL კოორდინატები. როგორც უკვე აღვნიშნეთ, პროგრამისტი თავად ახორციელებს მატრიცის ოპერაციების მოდულს. ბრუნვის მატრიცების ფორმირება, პროექციის მატრიცების ფორმირება, შებრუნებული მატრიცის ძიება, მატრიცის გამრავლება არის მინიმალური ნაკრებიმატრიცული ოპერაციების მოდულში შემავალი ოპერაციები. ჩნდება ორი ლოგიკური კითხვა. თუ ხილვადობის მოცულობა არის კუბი, რომლის კიდის სიგრძე უდრის ორს, მაშინ რატომ ჩანს სცენა რამდენიმე ათასი ერთეულის ზომით ეკრანზე? რა მომენტში გარდაიქმნება მომხმარებლის კოორდინატთა სისტემა CVV კოორდინატულ სისტემად? საპროექციო მატრიცები სწორედ ის ერთეულია, რომელიც ეხება ამ საკითხებს.

ზემოაღნიშნულის მთავარი იდეა ისაა, რომ დეველოპერს თავად შეუძლია აირჩიოს მომხმარებლის კოორდინატთა სისტემის ტიპი და სწორად უნდა აღწეროს პროექციის მატრიცები. ეს ავსებს ფაქტებს OpenGL-ის შესახებ და დროა გავაერთიანოთ ყველაფერი.

ერთ-ერთი ყველაზე გავრცელებული და რთულად აღსაქმელი მატრიცაა პერსპექტიული ტრანსფორმაციის მატრიცა. როგორ უკავშირდება ის CVV-ს და მომხმარებლის კოორდინატულ სისტემას? რატომ ხდება ობიექტები უფრო პატარა, როდესაც იზრდება მათი მანძილი დამკვირვებლისგან? იმის გასაგებად, თუ რატომ მცირდება ობიექტები მანძილის ზრდასთან ერთად, მოდით შევხედოთ მატრიცის გარდაქმნებს სამგანზომილებიანი მოდელინაბიჯ - ნაბიჯ. საიდუმლო არ არის, რომ ნებისმიერი სამგანზომილებიანი მოდელი შედგება წვეროების სასრული სიისგან, რომლებიც ერთმანეთისგან სრულიად დამოუკიდებლად განიცდიან მატრიცის გარდაქმნებს. ორგანზომილებიანი მონიტორის ეკრანზე სამგანზომილებიანი წვერის კოორდინატის დასადგენად, საჭიროა:

დეკარტის კოორდინატის გადაყვანა ერთგვაროვან კოორდინატად;
გაამრავლეთ ერთგვაროვანი კოორდინატი მოდელის მატრიცით;
შედეგი მრავლდება ხედვის მატრიცით;
შედეგის გამრავლება პროექციის მატრიცით;
მიღებული შედეგი გადააქციეთ ერთგვაროვანი კოორდინატებიდან დეკარტის კოორდინატებად.

ადრე განვიხილეთ დეკარტის კოორდინატების ერთგვაროვან კოორდინატებად გადაქცევა. მოდელის მატრიცის გეომეტრიული მნიშვნელობა არის მოდელის თარგმნა ლოკალური სისტემაკოორდინატები შიგნით გლობალური სისტემაკოორდინატები ან, როგორც ამბობენ, გადაიტანეთ წვეროები მოდელის სივრციდან მსოფლიო სივრცეში. მარტივად რომ ვთქვათ, ფაილიდან დატვირთული სამგანზომილებიანი ობიექტი მდებარეობს მოდელის სივრცეში, სადაც კოორდინატები იზომება თავად ობიექტთან შედარებით. შემდეგი, მოდელის მატრიცის გამოყენებით, მოდელი განლაგებულია, მასშტაბირებული და ბრუნავს. შედეგად, სამგანზომილებიანი მოდელის ყველა წვერო იღებს რეალურ ერთგვაროვან კოორდინატებს სამგანზომილებიანი სცენა. მოდელის სივრცე მსოფლიო სივრცესთან შედარებით ლოკალურია. მოდელის სივრციდან კოორდინატები გადადის მსოფლიო სივრცეში (ლოკალურიდან გლობალურში). ამ მიზნით გამოიყენება მოდელის მატრიცა.

ახლა გადავიდეთ მესამე საფეხურზე. სწორედ აქ მოქმედებს ხედვის სივრცე. ამ სივრცეში კოორდინატები იზომება დამკვირვებლის პოზიციისა და ორიენტაციის მიმართ, თითქოს ის იყოს სამყაროს ცენტრი. ხედვის სივრცე ლოკალურია მსოფლიო სივრცის მიმართ, ამიტომ მასში კოორდინატები უნდა იყოს შეყვანილი (და არა ამოღებული, როგორც წინა შემთხვევაში). პირდაპირი მატრიცის ტრანსფორმაცია შლის კოორდინატებს გარკვეული სივრციდან. იმისათვის, რომ პირიქით, შევიტანოთ ისინი, აუცილებელია მატრიცის ტრანსფორმაციის ინვერსია, ამიტომ ტიპის ტრანსფორმაცია აღწერილია შებრუნებული მატრიცით. როგორ მივიღოთ ეს ინვერსიული მატრიცა? პირველი, მოდით მივიღოთ პირდაპირი დამკვირვებლის მატრიცა. რა ახასიათებს დამკვირვებელს? დამკვირვებელი აღწერილია კოორდინატით, რომელშიც ის მდებარეობს და ნახვის მიმართულების ვექტორებით. დამკვირვებელი ყოველთვის იყურება თავისი ადგილობრივი ღერძის მიმართულებით ზ. დამკვირვებელს შეუძლია სცენის გარშემო გადაადგილება და მონაცვლეობა. მრავალი თვალსაზრისით, ეს ჰგავს მოდელის მატრიცის მნიშვნელობას. ზოგადად, ასეა. თუმცა დამკვირვებლისთვის სკალირების ოპერაცია უაზროა, შესაბამისად, დამკვირვებლის მოდელის მატრიცასა და სამგანზომილებიანი ობიექტის მოდელის მატრიცას შორის ტოლობის ნიშანი არ შეიძლება. დამკვირვებლის მოდელის მატრიცა არის სასურველი პირდაპირი მატრიცა. ამ მატრიცის ინვერსიით ვიღებთ ხედვის მატრიცას. პრაქტიკაში, ეს ნიშნავს, რომ გლობალურ ერთგვაროვან კოორდინატებში ყველა წვერო მიიღებს ახალ ჰომოგენურ კოორდინატებს დამკვირვებლის მიმართ. შესაბამისად, თუ დამკვირვებელმა დაინახა გარკვეული წვერო, მაშინ ერთგვაროვანი კოორდინატის მნიშვნელობა ზმოცემული წვეროს ხედვის სივრცეში აუცილებლად დადებითი რიცხვი იქნება. თუ წვერო დამკვირვებლის უკან იყო, მაშინ მისი ერთგვაროვანი კოორდინატის მნიშვნელობა ზხედვის სივრცეში აუცილებლად უარყოფითი რიცხვი იქნება.

მეოთხე ნაბიჯი ყველაზე საინტერესო ნაბიჯია. წინა ნაბიჯებიგანზრახ განიხილეს ისე დეტალურად, რომ მკითხველს ჰქონდეს სრული სურათი მეოთხე საფეხურის ყველა ოპერანდზე. მეოთხე საფეხურზე ჰომოგენური კოორდინატები ხედვის სივრციდან CVV სივრცეში გადადის. კიდევ ერთხელ ხაზგასმულია ის ფაქტი, რომ ყველა პოტენციურად ხილულ წვეროს ექნება ერთგვაროვანი კოორდინატის დადებითი მნიშვნელობა. ზ.

განვიხილოთ ფორმის მატრიცა:

და წერტილი დამკვირვებლის ერთგვაროვან სივრცეში:

მოდით გავამრავლოთ ერთგვაროვანი კოორდინატი მოცემულ მატრიცზე:

გადავიყვანოთ მიღებული ერთგვაროვანი კოორდინატები დეკარტის კოორდინატებად:

ვთქვათ, არსებობს ორი წერტილი ხედვის სივრცეში ერთი და იგივე კოორდინატებით xდა წ, მაგრამ განსხვავებული კოორდინატებით ზ. სხვა სიტყვებით რომ ვთქვათ, ერთი წერტილი მეორეს ჩამორჩება. იმის გამო პერსპექტივის დამახინჯებადამკვირვებელმა უნდა დაინახოს ორივე წერტილი. მართლაც, ფორმულიდან ირკვევა, რომ კოორდინატზე გაყოფის გამო ზ, შეკუმშვა ხდება საწყის წერტილამდე. რაც უფრო მაღალია ღირებულება ზ(რაც უფრო შორს არის წერტილი დამკვირვებლისგან), მით უფრო ძლიერია შეკუმშვა. ეს არის პერსპექტიული ეფექტის ახსნა.

OpenGL-ის სპეციფიკაციაში ნათქვამია, რომ ამოკვეთისა და რასტერიზაციის ოპერაციები შესრულებულია დეკარტის კოორდინატებში, ხოლო ერთგვაროვანი კოორდინატების დეკარტის კოორდინატებად გარდაქმნის პროცესი ავტომატურად ხდება.

მატრიცა (1) არის პერსპექტიული პროექციის მატრიცის შაბლონი. როგორც უკვე აღვნიშნეთ, პროექციის მატრიცის ამოცანა შედგება ორი წერტილისგან: მომხმარებლის კოორდინატთა სისტემის დაყენება (მარცხენა ან მემარჯვენე), დამკვირვებლის ხილვადობის მოცულობის CVV-ზე გადატანა. მოდით გამოვიტანოთ პერსპექტივის მატრიცა მარცხენა მომხმარებლის კოორდინატთა სისტემისთვის.

პროექციის მატრიცის აღწერა შესაძლებელია ოთხის დახმარებითპარამეტრები (ნახ. 3):

ხედვის კუთხე რადიანებში ( ფოვი);
ასპექტის თანაფარდობა ( ასპექტი);
მანძილი უახლოეს საჭრელ თვითმფრინავამდე ( ნ);
მანძილი შორს ამოკვეთის თვითმფრინავამდე ( ვ).

ბრინჯი. 3. ხილვადობის პერსპექტიული მოცულობა

განვიხილოთ წერტილის პროექცია დამკვირვებლის სივრცეში ხილვადობის პერსპექტიული მოცულობის კვეთის წინა კიდეზე. მეტი სიცხადისთვის, ნახ. 4 გვიჩვენებს გვერდით ხედს. გასათვალისწინებელია ისიც, რომ მომხმარებლის კოორდინატთა სისტემა ემთხვევა CVV კოორდინატთა სისტემას, ანუ ყველგან გამოიყენება მარცხენა კოორდინატთა სისტემა.

ბრინჯი. 4. თვითნებური წერტილის პროექცია

მსგავსი სამკუთხედების თვისებებზე დაყრდნობით, ჭეშმარიტია შემდეგი ტოლობები:

მოდით გამოვხატოთ yꞌ და xꞌ:

პრინციპში, გამონათქვამები (2) საკმარისია პროექციის წერტილების კოორდინატების მისაღებად. თუმცა, სამგანზომილებიანი ობიექტების სწორად ეკრანიზაციისთვის, თქვენ უნდა იცოდეთ თითოეული ფრაგმენტის სიღრმე. სხვა სიტყვებით რომ ვთქვათ, აუცილებელია კომპონენტის ღირებულების შენახვა ზ. ეს არის მნიშვნელობა, რომელიც გამოიყენება OpenGL სიღრმის ტესტებისთვის. ნახ. 3 ცხადია, რომ ღირებულება zꞌარ არის შესაფერისი როგორც ფრაგმენტის სიღრმე, რადგან ყველა წერტილის პროგნოზს შეუძლია იგივე ღირებულება zꞌ. ამ სიტუაციიდან გამოსავალი არის ფსევდო სიღრმის ე.წ.

ფსევდო სიღრმის თვისებები:

ფსევდო სიღრმე გამოითვლება მნიშვნელობის მიხედვით ზ;
რაც უფრო ახლოს არის წერტილი დამკვირვებელთან, მით ნაკლები მნიშვნელობა აქვს ფსევდოღრმას;
ხილვადობის მოცულობის წინა სიბრტყეზე მდებარე ყველა წერტილს აქვს ფსევდო სიღრმის მნიშვნელობა -1;
ყველა წერტილს, რომელიც მდებარეობს ხილვადობის მოცულობის შორს ჭრის სიბრტყეზე, აქვს ფსევდოსიღრმის მნიშვნელობა 1;
ხილვადობის მოცულობის შიგნით მდებარე ყველა ფრაგმენტს აქვს ფსევდო სიღრმის მნიშვნელობა [-1 1] დიაპაზონში.

გამოვიტანოთ ფორმულა, რომლითაც გამოითვლება ფსევდო სიღრმე. საფუძვლად ავიღოთ შემდეგი გამოთქმა:

შანსები ადა ბსაჭიროებს გამოთვლას. ამისათვის ვიყენებთ ფსევდოსიღრმეების თვისებებს 3 და 4. ვიღებთ ორი განტოლების სისტემას ორი უცნობით:

დავამატოთ სისტემის ორივე ნაწილი და გავამრავლოთ შედეგი ნამრავლზე fn, სადაც ვდა ნარ შეიძლება იყოს ნულის ტოლი. ჩვენ ვიღებთ:

გავხსნათ ფრჩხილები და ვაწესრიგოთ ტერმინები ისე, რომ მხოლოდ ნაწილი ა, და მარჯვნივ მხოლოდ ბ:

ჩავანაცვლოთ (6) (5-ით). გადავიყვანოთ გამოხატულება მარტივ წილადად:

გავამრავლოთ ორივე მხარე -2fn, სადაც ვდა ნარ შეიძლება იყოს ნულის ტოლი. წარმოვადგინოთ მსგავსები, გადავაწყოთ ტერმინები და გამოვხატოთ ბ:

ჩავანაცვლოთ (7) (6)-ით და გამოვხატოთ ა:

შესაბამისად კომპონენტები ადა ბთანაბარია:

ახლა მოდით შევცვალოთ მიღებული კოეფიციენტები სამუშაო ნაწილის მატრიცაში (1) და ვნახოთ რა ბედი ეწევა კოორდინატს ზდამკვირვებლის ერთგვაროვან სივრცეში თვითნებური წერტილისთვის. ჩანაცვლება ხდება შემდეგნაირად:

დაუშვით მანძილი წინა საჭრელ სიბრტყემდე ნუდრის 2-ს და მანძილი შორს ამოკვეთის სიბრტყემდე ვუდრის 10. განვიხილოთ ხუთი წერტილი დამკვირვებლის ერთგვაროვან სივრცეში:

წერტილის ფარდობითი პოზიცია და ხილვადობის მოცულობა

Წერტილი	მნიშვნელობა	აღწერა
1	1	წერტილი განლაგებულია ხილვადობის მოცულობის წინა მოჭრილი სიბრტყის წინ. არ გადის რასტერიზაციას.
2	2	წერტილი მდებარეობს ხილვადობის მოცულობის წყვეტის წინა კიდეზე. გადის რასტერიზაცია.
3	5	წერტილი განლაგებულია ხილვადობის მოცულობის წინა დაჭერის კიდეს შორის. გადის რასტერიზაცია.
4	10	წერტილი მდებარეობს ხილვადობის მოცულობის შეწყვეტის შორს კიდეზე. გადის რასტერიზაცია.
5	20	წერტილი მდებარეობს ხილვადობის მოცულობის წყვეტის შორს კიდის მიღმა. არ გადის რასტერიზაციას.

მოდით გავამრავლოთ ყველა წერტილი მატრიცით (8) და შემდეგ მივიღოთ მიღებული ერთგვაროვანი კოორდინატები დეკარტის კოორდინატებად . ამისათვის ჩვენ უნდა გამოვთვალოთ ახალი ერთგვაროვანი კომპონენტების მნიშვნელობები და .
წერტილი 1:

გაითვალისწინეთ, რომ ერთგვაროვანი კოორდინატი აბსოლუტურად სწორად არის განლაგებული CVV-ში და რაც მთავარია, OpenGL სიღრმის ტესტი უკვე შესაძლებელია, რადგან ფსევდო სიღრმე სრულად აკმაყოფილებს ტესტის მოთხოვნებს.

კოორდინატით ზჩვენ გავარკვიეთ, გადავიდეთ კოორდინატებზე xდა წ. როგორც უკვე აღვნიშნეთ, ხილვადობის მთელი პერსპექტიული მოცულობა უნდა შეესაბამებოდეს CVV-ს. CVV კიდეის სიგრძე ორია. შესაბამისად, ხილვადობის პერსპექტიული მოცულობის სიმაღლე და სიგანე უნდა იყოს შეკუმშული ორ ჩვეულებრივ ერთეულზე.

ჩვენს განკარგულებაშია კუთხე ფოვიდა სიდიდე ასპექტი. მოდით გამოვხატოთ სიმაღლე და სიგანე ამ მნიშვნელობების გამოყენებით.

ბრინჯი. 5. ხილვადობის მოცულობა

ნახ. 5 ცხადია, რომ:

ახლა ჩვენ შეგვიძლია მივიღოთ პერსპექტიული პროექციის მატრიცის საბოლოო ხედვა მორგებული მარცხენა კოორდინატთა სისტემისთვის, რომელიც მუშაობს CVV OpenGL-თან:

ეს ასრულებს მატრიცების წარმოქმნას.

ორიოდე სიტყვა DirectX-ის შესახებ - OpenGL-ის მთავარი კონკურენტი. DirectX განსხვავდება OpenGL-ისგან მხოლოდ CVV-ის ზომებითა და მისი პოზიციონირებით. DirectX-ში CVV არის მართკუთხა პარალელეპიპედი სიგრძით მისი ღერძების გასწვრივ xდა წუდრის ორს და ღერძის გასწვრივ ზსიგრძე ერთის ტოლია. Დიაპაზონი xდა წარის [-1 1] და დიაპაზონი ზტოლია . რაც შეეხება CVV კოორდინატთა სისტემას, DirectX, ისევე როგორც OpenGL, იყენებს მარცხენა კოორდინატთა სისტემას.

პერსპექტიული მატრიცების საჩვენებლად მორგებული მარჯვენა კოორდინატთა სისტემისთვის, თქვენ უნდა გადახაზოთ ნახ. 2, სურ. 3 და ნახ. 4 ახალი ღერძის მიმართულების გათვალისწინებით ზ. შემდგომი გამოთვლები სრულიად მსგავსია, ნიშანმდე. DirectX მატრიცებისთვის, ფსევდო სიღრმის თვისებები 3 და 4 შეცვლილია დიაპაზონისთვის.

ამ ეტაპზე, პერსპექტიული მატრიცების თემა შეიძლება ჩაითვალოს დახურულად.

ბოლო ლექციაზე ვისაუბრეთ აფინურ გეომეტრიაში გამოყენებულ ყველაზე მნიშვნელოვან პროექციებზე. მოდით გადავიდეთ პერსპექტიული გეომეტრიის და რამდენიმე ახალი ტიპის პროექციის განხილვაზე.

ფოტოებზე, ნახატებსა და ეკრანებზე გამოსახულებები ბუნებრივად და სწორად გვეჩვენება. ამ სურათებს პერსპექტივა ეწოდება. მათი თვისებები ისეთია, რომ უფრო შორეული ობიექტები გამოსახულია უფრო მცირე მასშტაბით, პარალელური ხაზებით. ზოგადი შემთხვევაარ არიან პარალელური. შედეგად, გამოსახულების გეომეტრია საკმაოდ რთული აღმოჩნდება და დასრულებული სურათიძნელია ობიექტის გარკვეული ნაწილების ზომის განსაზღვრა.

ჩვეულებრივი პერსპექტიული პროექცია არის ცენტრალური პროექცია სიბრტყეზე სწორი სხივებით, რომელიც გადის წერტილში, პროექციის ცენტრში. ერთ-ერთი გამოსხივებული სხივი პროექციის სიბრტყის პერპენდიკულარულია და მას მთავარი ეწოდება. ამ სხივისა და პროექციის სიბრტყის გადაკვეთის წერტილი არის სურათის მთავარი წერტილი.

არსებობს სამი კოორდინატთა სისტემა. როგორც წესი, პროგრამისტი მუშაობს და ინახავს მონაცემებს გეომეტრიული ობიექტების შესახებ მსოფლიო კოორდინატებში. რეალიზმის გასაზრდელად, ეკრანზე გამოსახულების გამოსატანად მომზადებისას, ობიექტების შესახებ მონაცემები მსოფლიო კოორდინატებიდან გარდაიქმნება სანახავად. და მხოლოდ იმ მომენტში, როდესაც სურათი პირდაპირ ეკრანზე გამოჩნდება, ისინი გადადიან ეკრანის კოორდინატებზე, რაც არის ეკრანის პიქსელების რიცხვები.

პირველი ორი სისტემა შეიძლება გამოყენებულ იქნას მრავალგანზომილებიან კოორდინატულ სისტემებში, მაგრამ ეს უკანასკნელი მხოლოდ ორგანზომილებიანში. ოპერაციები შეუქცევადია, ანუ შეუძლებელია სამგანზომილებიანი გამოსახულების აღდგენა ორგანზომილებიანი პროექციის გამოსახულებისგან.

ზოგადი პერსპექტივის ტრანსფორმაციის მატრიცა

ამ მატრიცაში ელემენტები ა, დ, ეპასუხისმგებელნი არიან სკალირებაზე, მ, ნ, ლგადაადგილებისთვის, გვ, ქ, რპროექციისთვის, სყოვლისმომცველი სკალირებისთვის, Xბრუნვისთვის.

ეს არ არის პრობლემის გადაწყვეტა! მოდით ერთად გავარკვიოთ!

მოდით ვიყოთ რეალისტები პრაქტიკული მიკერძოებით და ავიღოთ OpenGL ვერსია 3.3, როგორც ტესტის საგანი. ამ ვერსიიდან დაწყებული, თითოეულ დეველოპერს მოეთხოვება დამოუკიდებლად განახორციელოს მატრიცის ოპერაციების მოდული. კარგია, ეს არის ის, რაც ჩვენ გვჭირდება. მოდით დავშალოთ ჩვენი რთული ამოცანა და გამოვყოთ ძირითადი პუნქტები. ზოგიერთი ფაქტი OpenGL სპეციფიკაციიდან:

მატრიცები ინახება სვეტებში (სვეტი-ძირითადი);
ერთგვაროვანი კოორდინატები;
კანონიკური ამოკვეთის მოცულობა (CVV) მარცხენა კოორდინატულ სისტემაში.

მატრიცების შესანახად ორი გზა არსებობს: სვეტი-მაჟორი და მწკრივი-მაჟორი. წრფივი ალგებრაზე ლექციებში გამოიყენება მწკრივის ძირითადი სქემა. ზოგადად, მეხსიერებაში მატრიცების წარმოდგენას მნიშვნელობა არ აქვს, რადგან მატრიცა ყოველთვის შეიძლება გადაიზარდოს ერთი ტიპის წარმოდგენიდან მეორეზე მარტივი ტრანსპოზიციით. და რადგან განსხვავება არ არის, მაშინ ყველა შემდგომი გამოთვლებისთვის ჩვენ გამოვიყენებთ კლასიკურ მწკრივის ძირითად მატრიცებს. OpenGL-ის პროგრამირებისას არის პატარა ხრიკი, რომელიც საშუალებას გაძლევთ თავიდან აიცილოთ მატრიცების ტრანსპონირება კლასიკური მწკრივის ძირითადი გამოთვლების შენარჩუნებისას. მატრიცა უნდა გადავიდეს შადერის პროგრამაში, როგორც არის, ხოლო ჩრდილში გამრავლება უნდა განხორციელდეს არა ვექტორსა და მატრიცას შორის, არამედ მატრიცასა და ვექტორს შორის.

ერთგვაროვანი კოორდინატები არ არის ძალიან სახიფათო სისტემა მრავალი მარტივი წესით ნაცნობი დეკარტის კოორდინატების ერთგვაროვან კოორდინატებად გადაქცევისთვის და პირიქით. ერთგვაროვანი კოორდინატი არის განზომილების მწკრივის მატრიცა. დეკარტის კოორდინატის ერთგვაროვან კოორდინატად გადაქცევისთვის აუცილებელია x, წდა ზგავამრავლოთ ნებისმიერ რეალურ რიცხვზე ვ(0-ის გარდა). შემდეგი, თქვენ უნდა ჩაწეროთ შედეგი პირველ სამ კომპონენტში, ხოლო ბოლო კომპონენტი ტოლი იქნება მულტიპლიკატორის ვ. Სხვა სიტყვებით:
- დეკარტის კოორდინატები
ვ- რეალური რიცხვი არ უდრის 0-ს

- ერთგვაროვანი კოორდინატები

წვეროების საპირისპირო გადათარგმნა ერთგვაროვანი კოორდინატებიდან დეკარტის კოორდინატებზე ხორციელდება შემდეგნაირად. მწკრივის მატრიცის ყველა კომპონენტი უნდა გაიყოს ბოლო კომპონენტზე. Სხვა სიტყვებით:

- ერთგვაროვანი კოორდინატები
- დეკარტის კოორდინატები

ბრინჯი. 1. კანონიკური OpenGL ამოკვეთის მოცულობა (CVV)

ბრინჯი. 2. საკოორდინაციო სისტემები

როგორც ჩანს ნახ. 2 კოორდინატთა სისტემა განსხვავდება მხოლოდ ღერძის მიმართულებით ზ. OpenGL 1.0 იყენებს მომხმარებლის მარჯვენა კოორდინატულ სისტემას. მაგრამ CVV კოორდინატთა სისტემა და მომხმარებლის კოორდინატთა სისტემა ორი სრულიად განსხვავებული რამ არის. უფრო მეტიც, 3.3 ვერსიის მიხედვით, აღარ არსებობს სტანდარტული OpenGL კოორდინატთა სისტემა. როგორც უკვე აღვნიშნეთ, პროგრამისტი თავად ახორციელებს მატრიცის ოპერაციების მოდულს. ბრუნვის მატრიცების ფორმირება, პროექციის მატრიცების ფორმირება, შებრუნებული მატრიცის ძიება, მატრიცების გამრავლება - ეს არის მატრიცის ოპერაციების მოდულში შემავალი ოპერაციების მინიმალური ნაკრები. ჩნდება ორი ლოგიკური კითხვა. თუ ხილვადობის მოცულობა არის კუბი, რომლის კიდის სიგრძე უდრის ორს, მაშინ რატომ ჩანს სცენა რამდენიმე ათასი ერთეულის ზომით ეკრანზე? რა მომენტში გარდაიქმნება მომხმარებლის კოორდინატთა სისტემა CVV კოორდინატულ სისტემად? საპროექციო მატრიცები სწორედ ის ერთეულია, რომელიც ეხება ამ საკითხებს.

ერთ-ერთი ყველაზე გავრცელებული და რთულად აღსაქმელი მატრიცაა პერსპექტიული ტრანსფორმაციის მატრიცა. როგორ უკავშირდება ის CVV-ს და მომხმარებლის კოორდინატულ სისტემას? რატომ ხდება ობიექტები უფრო პატარა, როდესაც იზრდება მათი მანძილი დამკვირვებლისგან? იმის გასაგებად, თუ რატომ იკუმშება ობიექტები მანძილის ზრდასთან ერთად, მოდით გადავხედოთ 3D მოდელის მატრიცულ გარდაქმნებს ეტაპობრივად. საიდუმლო არ არის, რომ ნებისმიერი სამგანზომილებიანი მოდელი შედგება წვეროების სასრული სიისგან, რომლებიც ერთმანეთისგან სრულიად დამოუკიდებლად განიცდიან მატრიცის გარდაქმნებს. ორგანზომილებიანი მონიტორის ეკრანზე სამგანზომილებიანი წვერის კოორდინატის დასადგენად, საჭიროა:

დეკარტის კოორდინატის გადაყვანა ერთგვაროვან კოორდინატად;
გაამრავლეთ ერთგვაროვანი კოორდინატი მოდელის მატრიცით;
შედეგი მრავლდება ხედვის მატრიცით;
შედეგის გამრავლება პროექციის მატრიცით;
მიღებული შედეგი გადააქციეთ ერთგვაროვანი კოორდინატებიდან დეკარტის კოორდინატებად.

ადრე განვიხილეთ დეკარტის კოორდინატების ერთგვაროვან კოორდინატებად გადაქცევა. მოდელის მატრიცის გეომეტრიული მნიშვნელობა არის მოდელის გადატანა ადგილობრივი კოორდინატთა სისტემიდან გლობალურ კოორდინატულ სისტემაში. ან, როგორც ამბობენ, გადაიტანეთ წვეროები მოდელის სივრციდან მსოფლიო სივრცეში. მარტივად რომ ვთქვათ, ფაილიდან დატვირთული სამგანზომილებიანი ობიექტი მდებარეობს მოდელის სივრცეში, სადაც კოორდინატები იზომება თავად ობიექტთან შედარებით. შემდეგი, მოდელის მატრიცის გამოყენებით, მოდელი განლაგებულია, მასშტაბირებული და ბრუნავს. შედეგად, 3D მოდელის ყველა წვერო იღებს ფაქტობრივ ერთგვაროვან კოორდინატებს 3D სცენაზე. მოდელის სივრცე მსოფლიო სივრცესთან შედარებით ლოკალურია. მოდელის სივრციდან კოორდინატები გადადის მსოფლიო სივრცეში (ლოკალურიდან გლობალურში). ამ მიზნით გამოიყენება მოდელის მატრიცა.

მეოთხე ნაბიჯი ყველაზე საინტერესო ნაბიჯია. წინა საფეხურები ისე დეტალურად იქნა განხილული მიზანმიმართულად, რათა მკითხველს ჰქონდეს სრული სურათი მეოთხე საფეხურის ყველა ოპერანდზე. მეოთხე საფეხურზე ჰომოგენური კოორდინატები ხედვის სივრციდან CVV სივრცეში გადადის. კიდევ ერთხელ ხაზგასმულია ის ფაქტი, რომ ყველა პოტენციურად ხილულ წვეროს ექნება ერთგვაროვანი კოორდინატის დადებითი მნიშვნელობა. ზ.

განვიხილოთ ფორმის მატრიცა:

და წერტილი დამკვირვებლის ერთგვაროვან სივრცეში:

მოდით გავამრავლოთ ერთგვაროვანი კოორდინატი მოცემულ მატრიცზე:

ვთქვათ, არსებობს ორი წერტილი ხედვის სივრცეში ერთი და იგივე კოორდინატებით xდა წ, მაგრამ განსხვავებული კოორდინატებით ზ. სხვა სიტყვებით რომ ვთქვათ, ერთი წერტილი მეორეს ჩამორჩება. პერსპექტივის დამახინჯების გამო დამკვირვებელმა ორივე წერტილი უნდა დაინახოს. მართლაც, ფორმულიდან ირკვევა, რომ კოორდინატზე გაყოფის გამო ზ, შეკუმშვა ხდება საწყის წერტილამდე. რაც უფრო მაღალია ღირებულება ზ(რაც უფრო შორს არის წერტილი დამკვირვებლისგან), მით უფრო ძლიერია შეკუმშვა. ეს არის პერსპექტიული ეფექტის ახსნა.

პროექციის მატრიცა შეიძლება აღწერილი იყოს ოთხი პარამეტრის გამოყენებით (ნახ. 3):

ხედვის კუთხე რადიანებში ( ფოვი);
ასპექტის თანაფარდობა ( ასპექტი);
მანძილი უახლოეს საჭრელ თვითმფრინავამდე ( ნ);
მანძილი შორს ამოკვეთის თვითმფრინავამდე ( ვ).

ბრინჯი. 3. ხილვადობის პერსპექტიული მოცულობა

ბრინჯი. 4. თვითნებური წერტილის პროექცია

მოდით გამოვხატოთ yꞌ და xꞌ:

პრინციპში, გამონათქვამები (2) საკმარისია პროექციის წერტილების კოორდინატების მისაღებად. თუმცა, სამგანზომილებიანი ობიექტების სწორად ეკრანიზაციისთვის, თქვენ უნდა იცოდეთ თითოეული ფრაგმენტის სიღრმე. სხვა სიტყვებით რომ ვთქვათ, აუცილებელია კომპონენტის ღირებულების შენახვა ზ. ეს არის მნიშვნელობა, რომელიც გამოიყენება OpenGL სიღრმის ტესტებისთვის. ნახ. 3 ცხადია, რომ ღირებულება zꞌარ არის შესაფერისი როგორც ფრაგმენტის სიღრმე, რადგან ყველა წერტილის პროგნოზს აქვს იგივე მნიშვნელობა zꞌ. ამ სიტუაციიდან გამოსავალი არის ფსევდო სიღრმის ე.წ.

ფსევდო სიღრმის თვისებები:

ფსევდო სიღრმე გამოითვლება მნიშვნელობის მიხედვით ზ;
რაც უფრო ახლოს არის წერტილი დამკვირვებელთან, მით ნაკლები მნიშვნელობა აქვს ფსევდოღრმას;
ხილვადობის მოცულობის წინა სიბრტყეზე მდებარე ყველა წერტილს აქვს ფსევდო სიღრმის მნიშვნელობა -1;
ყველა წერტილს, რომელიც მდებარეობს ხილვადობის მოცულობის შორს ჭრის სიბრტყეზე, აქვს ფსევდოსიღრმის მნიშვნელობა 1;
ხილვადობის მოცულობის შიგნით მდებარე ყველა ფრაგმენტს აქვს ფსევდო სიღრმის მნიშვნელობა [-1 1] დიაპაზონში.

ჩავანაცვლოთ (6) (5-ით). გადავიყვანოთ გამოხატულება მარტივ წილადად:

ჩავანაცვლოთ (7) (6)-ით და გამოვხატოთ ა:

შესაბამისად კომპონენტები ადა ბთანაბარია:

წერტილის ფარდობითი პოზიცია და ხილვადობის მოცულობა

Წერტილი	მნიშვნელობა	აღწერა
1	1	წერტილი განლაგებულია ხილვადობის მოცულობის წინა მოჭრილი სიბრტყის წინ. არ გადის რასტერიზაციას.
2	2	წერტილი მდებარეობს ხილვადობის მოცულობის წყვეტის წინა კიდეზე. გადის რასტერიზაცია.
3	5	წერტილი განლაგებულია ხილვადობის მოცულობის წინა დაჭერის კიდეს შორის. გადის რასტერიზაცია.
4	10	წერტილი მდებარეობს ხილვადობის მოცულობის შეწყვეტის შორს კიდეზე. გადის რასტერიზაცია.
5	20	წერტილი მდებარეობს ხილვადობის მოცულობის წყვეტის შორს კიდის მიღმა. არ გადის რასტერიზაციას.

ბრინჯი. 5. ხილვადობის მოცულობა

ნახ. 5 ცხადია, რომ:

ეს ასრულებს მატრიცების წარმოქმნას.

ამ ეტაპზე, პერსპექტიული მატრიცების თემა შეიძლება ჩაითვალოს დახურულად.

დღეს ჩვენ უფრო დეტალურად განვიხილავთ ვირტუალური კამერის მოწყობილობას. დავიწყოთ სურათით.

სურათზე ჩვენ ვხედავთ კამერის კოორდინატთა სივრცეს. კამერის მიმართულება („გამოხედვა“) ყოველთვის ემთხვევა z-ღერძის დადებით მიმართულებას და თავად კამერა მდებარეობს საწყისზე.

ფიგურაში ნაჩვენები პირამიდის შიდა სივრცე არის ვირტუალური სამყაროს ის ნაწილი, რომელსაც მომხმარებელი დაინახავს.

ყურადღება მიაქციეთ სამ თვითმფრინავს. პირველი მდებარეობს z ღერძის გასწვრივ 1 მანძილზე. ეს არის ახლო თვითმფრინავი. მოთამაშე ვერასოდეს დაინახავს იმას, რაც მის წინ არის. IN ამ შემთხვევაში z-ის მნიშვნელობა ერთის ტოლია, მაგრამ ზოგადად, ეს შეიძლება იყოს ნებისმიერი. ერთი გრაფიკული დისპლეის დეფექტი დაკავშირებულია ახლო თვითმფრინავთან. ეს დეფექტი ვლინდება პირველ რიგში მსროლელებში (კამერის დიდი თავისუფლების გამო). როდესაც ძალიან მიუახლოვდებით ობიექტს, შეგიძლიათ მოხვდეთ "შიგნით". დან უახლესი თამაშებიეს დეფექტი განსაკუთრებით გამოხატული იყო Left 4 dead-ში: როდესაც ზომბების ბრბო ეცემა მოთამაშეს, ძალიან ხშირად შესაძლებელი იყო სხვა პერსონაჟების შიგნით შეხედვა.

z ღერძის გასწვრივ 100 ერთეულის მანძილზე მდებარე სიბრტყეს შორეული სიბრტყე ეწოდება. კიდევ ერთხელ, მნიშვნელობა შეიძლება იყოს თვითნებური. მომხმარებელი ვერასოდეს დაინახავს ობიექტებს, რომლებიც მდებარეობს ამ თვითმფრინავზე შორს.

ექვს სიბრტყეს, რომლებიც ზღუდავენ სივრცეს, რომელსაც მომხმარებელი დაინახავს, ეწოდება ამოკვეთის სიბრტყე: მარცხენა, მარჯვენა, ზედა, ქვედა, ახლო და შორს.

ახლო და შორს შორის მდებარე თვითმფრინავი არის პროექცია. შემდეგში ჩვენ განვათავსებთ ამ სიბრტყეს z=1-ზე, ე.ი. ის დაემთხვევა უახლოესს. აქ გამოვყავი ახლო და საპროექციო სიბრტყეები, რათა მეჩვენებინა, რომ ისინი ერთი და იგივე არ არის. საპროექციო სიბრტყე განკუთვნილია საბოლოო კოორდინატების ტრანსფორმაციისთვის: ტრანსფორმაცია სამგანზომილებიანი კამერის სივრციდან ორგანზომილებიან სივრცეში.

სწორედ პროექციის სიბრტყის წყალობით დაინახავს მომხმარებელი ვირტუალური სამყარო. სინამდვილეში, ეს თვითმფრინავი არის ის, რასაც მომხმარებელი დაინახავს. პროექციის სიბრტყე პირდაპირ კავშირშია ცნებებთან, როგორიცაა წინა/ფონური ბუფერები, პროგრამის ფანჯარა და მომხმარებლის ეკრანი. ყველა ეს კონცეფცია შეიძლება ჩაითვალოს მართკუთხა სურათად, რომელიც წარმოდგენილია კომპიუტერის მეხსიერებაში რიცხვების მასივით.

სამგანზომილებიანი სამყაროდან საპროექციო სიბრტყეზე კოორდინატების გადაქცევა ყველაზე რთულია ამ მომენტშიჩვენ მიერ იქნა შესწავლილი.

ხედვის ველი

ზემოთ მოცემულ ფიგურაში, პროექციის სიბრტყეს (და შესაბამისად სურათს, რომელსაც მომხმარებელი დაინახავს) აქვს მის სიმაღლეზე მეტი სიგანე. პროექციის სიბრტყის სიგანე და სიმაღლე მითითებულია კუთხეების გამოყენებით. Შეხვედრა სხვადასხვა სახელებიეს კუთხეები: ხედვის არე ან ხედვის არე. ინგლისურად - ხედვის ველები.

სანახავი ადგილები მითითებულია ორი კუთხით. მოდით ვუწოდოთ მათ: fovx - ჰორიზონტალური სანახავი ზონა, fovy - ვერტიკალური სანახავი ზონა. დეტალები სანახავი ადგილების შესახებ: ქვემოთ.

Z-ბუფერი / w-ბუფერი / სიღრმის ბუფერი (z-ბუფერი / w-ბუფერი / სიღრმის ბუფერი)

მოდით შევხედოთ სურათს, რომელშიც ნაჩვენებია ორი სამკუთხედი: კამერიდან 25 და 50 ერთეულის დაშორებით. ნახაზი (a) გვიჩვენებს სამკუთხედების მდებარეობას სივრცეში (ზედა ხედი), ხოლო ფიგურა (ბ) აჩვენებს საბოლოო სურათს:

როგორც თქვენ ალბათ მიხვდებით, გამოსახულება უნდა იყოს დახატული, დაწყებული ყველაზე შორეული ელემენტებით და დამთავრებული უახლოესი ელემენტებით. აშკარა გამოსავალია გამოვთვალოთ მანძილი საწყისიდან (კამერიდან) თითოეულ ობიექტამდე და შემდეგ შევადაროთ. კომპიუტერული გრაფიკა იყენებს ოდნავ უფრო მოწინავე მექანიზმს. ამ მექანიზმს რამდენიმე სახელი აქვს: z-buffer, w-buffer, depth buffer. z-ბუფერის ზომა ელემენტების რაოდენობის მიხედვით იგივეა, რაც ფონის და ძირითადი ბუფერების ზომა. კამერასთან ყველაზე ახლოს მდებარე ობიექტის z-კომპონენტი შედის z-ბუფერში. IN ამ მაგალითში, სადაც ლურჯი სამკუთხედი გადაფარავს მწვანეს, ლურჯის z-კოორდინატები შეიტანება სიღრმის ბუფერში. z-ბუფერებზე უფრო დეტალურად ცალკე გაკვეთილზე ვისაუბრებთ.

ორთოგრაფიული/პარალელური პროექცია

ოპერაციას, რომლის დროსაც სივრცის განზომილება მცირდება (იყო სამგანზომილებიანი სივრცე, ის ორგანზომილებიანი გახდა) პროექცია ეწოდება. უპირველეს ყოვლისა, ჩვენ გვაინტერესებს პერსპექტიული პროექცია, მაგრამ ჯერ გავეცნობით პარალელურს (პარალელური ანუ ორთოგრაფიული პროექცია).

პარალელური პროექციის გამოსათვლელად საკმარისია ზედმეტი კოორდინატის გაუქმება. თუ გვაქვს წერტილი სივრცეში [ 3 3 3 ], მაშინ z=1 სიბრტყეზე პარალელური პროექციით, ის დაპროექტდება წერტილში.

პერსპექტიული პროექცია საპროექციო სიბრტყეზე

ამ ტიპის პროექციაში ყველა ხაზი ერთ წერტილში იყრის თავს. ზუსტად ასე მუშაობს ჩვენი ხედვა. და სწორედ პერსპექტიული პროექციის დახმარებით ხდება ყველა თამაშში „ლუქის“ მოდელირება.

შეადარეთ ეს ნახატი წინა გაკვეთილის ერთგვაროვან კოორდინატებს. სამგანზომილებიანი სივრციდან ორგანზომილებიან სივრცეში გადასასვლელად, თქვენ უნდა გავყოთ ვექტორების პირველი ორი კომპონენტი მესამეზე: [ x/z y/z z/z ] = [ x/z y/z 1 ].

როგორც ზემოთ დავწერე, პროექციის სიბრტყე შეიძლება განთავსდეს სადმე ახლოს და შორს შორის. ჩვენ ყოველთვის განვათავსებთ პროექციის სიბრტყეს z=1-ზე, მაგრამ ამ ტუტორიალში განვიხილავთ სხვა ვარიანტებს. მოდით შევხედოთ სურათს:

კოორდინატების წარმოშობიდან პროექციის სიბრტყემდე მანძილი დ-ით აღვნიშნოთ. განვიხილავთ ორ შემთხვევას: d=1 და d=5. მნიშვნელოვანი წერტილი: ყველა ვექტორის მესამე კომპონენტი პროექციის შემდეგ უნდა იყოს d-ის ტოლი - ყველა წერტილი განლაგებულია იმავე სიბრტყეში z=d. ამის მიღწევა შესაძლებელია ვექტორის ყველა კომპონენტის d-ზე გამრავლებით: [ xd/z yd/z zd/z ]. d=1-ით მივიღებთ: [ x/z y/z 1 ], ეს არის ფორმულა, რომელიც გამოიყენებოდა ერთგვაროვანი კოორდინატების გარდაქმნისთვის.

ახლა, თუ პროექციის სიბრტყეს გადავიტანთ z=5 წერტილში (შესაბამისად d=5), მივიღებთ: [ xd/z yd/z zd/z ] = [ 5x/z 5y/z 5 ]. ბოლო ფორმულა ასახავს სივრცის ყველა ვექტორს ერთ სიბრტყეში, სადაც d=5.
აქ ცოტა პრობლემა გვაქვს. წინა ფორმულა მუშაობს სამგანზომილებიანი ვექტორებით. მაგრამ ჩვენ შევთანხმდით ოთხგანზომილებიანი ვექტორების გამოყენებაზე. მეოთხე კომპონენტი ამ შემთხვევაში შეიძლება უბრალოდ გაუქმდეს. მაგრამ ჩვენ ამას არ გავაკეთებთ, რადგან მისი გამოყენება უზრუნველყოფს გარკვეულ შესაძლებლობებს, რომლებსაც მოგვიანებით განვიხილავთ.

თქვენ უნდა იპოვოთ მესამე და მეოთხე კომპონენტების საერთო გამყოფი, როდესაც იყოფა, რომლითაც მნიშვნელობა d რჩება მესამე კომპონენტში, ხოლო ერთიანობა მეოთხეში. ეს გამყოფი არის d/z. ახლა ჩვეულებრივი ვექტორიდან [ x y z 1 ] უნდა მივიღოთ პროექციისთვის (გაყოფისთვის) მზად ვექტორი [ x y z z/d ]. ეს კეთდება ტრანსფორმაციის მატრიცის გამოყენებით (შეამოწმეთ შედეგი რომელიმე ვექტორის ამ მატრიცზე გამრავლებით):

ბოლო ტრანსფორმაცია ჯერ არ არის პროექცია. აქ ჩვენ უბრალოდ ვამცირებთ ყველა ვექტორს ჩვენთვის საჭირო ფორმამდე. შეგახსენებთ, რომ პროექციის სიბრტყეს განვათავსებთ d=1-ზე, რაც ნიშნავს, რომ ვექტორები ასე გამოიყურება: [ x y z z ].

პერსპექტიული ტრანსფორმაციის მატრიცა

ჩვენ გადავხედავთ DirectX-ში გამოყენებულ პერსპექტივის ტრანსფორმაციის მატრიცას:

ახლა ჩვენ ვიცით, რა ელემენტისთვის არის განკუთვნილი _34. ჩვენ ასევე ვიცით, რომ ელემენტები _11 და _22 ადიდებენ სურათს ჰორიზონტალურად და ვერტიკალურად. მოდით შევხედოთ კონკრეტულად რა იმალება სახელების უკან xScale და yScale.

ეს ცვლადები დამოკიდებულია ხედვის არეებზე, რომლებიც ზემოთ განვიხილეთ. ამ კუთხეების გაზრდით ან შემცირებით, შეგიძლიათ სურათის მასშტაბირება (მასშტაბირება ან მასშტაბირება) - შეცვალოთ პროექციის სიბრტყის ზომა და ასპექტის თანაფარდობა. მასშტაბირების მექანიზმი ბუნდოვნად მოგვაგონებს კამერების/კამერების ზუმს - პრინციპი ძალიან ჰგავს. მოდით შევხედოთ სურათს:

მოდით გავყოთ კუთხე fov ორ ნაწილად და განვიხილოთ მხოლოდ ერთი ნახევარი. რასაც აქ ვხედავთ: კუთხის fov/2 (და შესაბამისად, კუთხის fov) გაზრდით, ჩვენ ვზრდით კუთხის sin და ვამცირებთ cos-ს. ეს იწვევს პროექციის სიბრტყის ზრდას და, შესაბამისად, დაპროექტებული ობიექტების შემცირებას. ჩვენთვის იდეალური კუთხე იქნება fov/2 = P/4. შეგახსენებთ, რომ კუთხე P/4 რადიანებში უდრის 45 გრადუსს. ამ შემთხვევაში, fov იქნება 90 გრადუსის ტოლი. რატომ არის ჩვენთვის კარგი 45 გრადუსიანი კუთხე? ამ შემთხვევაში არ არის მასშტაბირება და cos(P/4)/sin(P/4)=1.

ახლა ჩვენ შეგვიძლია მარტივად გავაფართოვოთ გამოსახულება ვერტიკალურად (ჰორიზონტალურად) ნახვის არეალის ნახევარის სინუსის და კოსინუსის გამოყენებით (კოტანგენტის ფუნქციას C++-ში ეწოდება cot):

yScale = cos(fovY/2)/sin(fovY/2) = cot(fovY/2)
DirectX იყენებს მხოლოდ ვერტიკალურ FOV-ს (fovY), ხოლო ჰორიზონტალური სკალირება დამოკიდებულია ვერტიკალურ FOV-ზე და ასპექტის თანაფარდობაზე.

შეგახსენებთ, რომ ჩვენს პროგრამებში ფანჯარა არის 500x500 ზომის. ასპექტის თანაფარდობა: 1-დან 1-მდე. შესაბამისად, ცვლადები ტოლი იქნება: xScale=1, yScale=1.

სტანდარტული მონიტორი/ტელევიზიის ასპექტის თანაფარდობა: 4:3. ეს თანაფარდობა შეესაბამება ეკრანის გარჩევადობას: 640x480, 800x600, 1600x1200. ჯერ არ შევეხებით სრული ეკრანის რეჟიმი, მაგრამ ჩვენ შეგვიძლია შევცვალოთ პროგრამის ფანჯრის ზომა. თქვენ შეგიძლიათ შეცვალოთ ფანჯრის ზომა (დღევანდელ პარამეტრებში), მაგალითად, 640X480. მაგრამ ყველა ობიექტის დაჭიმვის თავიდან ასაცილებლად (კვადრატები მართკუთხედებს ჰგავს), არ დაგავიწყდეთ პროექციის მატრიცაში შესაბამისი ცვლადების შეცვლა.

კინაღამ დამავიწყდა, ფორუმი xScale-ისთვის DirectX-ში:

xScale = yScale / ასპექტის თანაფარდობა
ასპექტის კოეფიციენტები დაყენებულია უბრალოდ: 1/1, 4/3, 16/9 - ეს არის სტანდარტული.

რჩება პერსპექტიული ტრანსფორმაციის მატრიცის _33, _34 ელემენტების დანიშნულების გარკვევა. zf არის შორეული სიბრტყის z-კოორდინატი (შორიდან - შორს), ხოლო zn არის ახლო სიბრტყის z-კოორდინატი (ახლოდან - ახლოს). გაითვალისწინეთ, რომ ელემენტი _43 = _33 * -zn.

ყველაზე მარტივი გზა იმის გასაგებად, თუ რას აკეთებენ ეს ფორმულები, არის მაგალითები. გავამრავლოთ სტანდარტული ვექტორი [ x y z w ] ზემოთ წარმოდგენილი მატრიცით. ამის გაკეთებას გირჩევთ ფურცლისა და ფანქრის აღებით (იმედია გახსოვთ, როგორ გავამრავლოთ ორი მატრიცა). ვექტორული კომპონენტები მიიღებენ შემდეგ ფორმას.

1 = x*xScale
მე-2 = y*yScale
მე-3 = z*(zf/(zf-zn)) + w*(-(zn*zf)/(zf-zn)) = (zf/(zf-zn))*(z - w*zn)
მე-4 = (w*z)/d
მოდით შევასრულოთ პროექციის ტრანსფორმაცია (ყველა ელემენტს ვყოფთ მე-4 კომპონენტად და დავუშვათ, რომ d=1 და w=1):

1 = (d*x*xScale)/(w*z) = (x*xScale)/z
მე-2 = (d*y*yScale)/(w*z) = (y*xScale)/z
3 = (zf/(zf-zn))*(z - w*zn)*(w*d/z) = (zf/(zf-zn))*(1 - zn/z)
მე-4 = 1
შედეგად მივიღეთ ფორმის ვექტორი:

[ x/(z*xScale) y/(z*yScale) (zf/(zf-zn))*(1-zn/z) 1 ]
ახლა, თუ დააკონკრეტებთ zf-სა და zn-ს კონკრეტულ მნიშვნელობებს, ნახავთ შემდეგს (დადებითი მნიშვნელობებისთვის): თუ ვექტორი მდებარეობს ახლო სიბრტყის წინ, მაშინ z-კომპონენტი ტრანსფორმაციის შემდეგ იქნება ნულზე ნაკლები, თუ ვექტორი მდებარეობს შორეული სიბრტყის უკან, მაშინ z-კომპონენტი იქნება უფრო დიდი ერთეული.

არ არის განსხვავება ზუსტად სად მდებარეობს ახლო და შორეული სიბრტყეები: zn=1, zf=10 ან zn=10 და zf=100 (ან სხვა მნიშვნელობები) - გარდაქმნის შემდეგ ხილული ფართობი განლაგდება ინტერვალში. ნულიდან ერთამდე ჩათვლით.

სწორედ ამაზეა გათვლილი პროექციის მატრიცის _33, _34 ელემენტებში არსებული ფორმულები - ახლოდან შორს სიბრტყემდე მანძილის პროექცია სეგმენტში. შეამოწმეთ ეს რამდენიმე ვექტორის მნიშვნელობების გამოთვლით კონკრეტული ღირებულებები zn,zf (დიახ, ფურცელზე!!!).

პროექციის მატრიცა. ზოგადი პერსპექტივის ტრანსფორმაციის მატრიცა. სრული პერსპექტივის პროექციის მოდელი

ერთგვაროვანი კოორდინატები

ტრანსფორმაციის მატრიცები

შესავალი მატრიცებში

გადაცემის მატრიცა

იდენტობის მატრიცა

სკალირების მატრიცა

ბრუნვის მატრიცა

გარდაქმნების გაერთიანება

სამყარო, ხედვა და პროექციის მატრიცები

მსოფლიო მატრიცა

მატრიცის ნახვა

პროექციის მატრიცა

ტრანსფორმაციების გაერთიანება: ModelViewProjection მატრიცა

ყველაფერს ერთად ათავსებ

Დავალებები

ზოგადი პერსპექტივის ტრანსფორმაციის მატრიცა

შეატყობინეთ შეცდომას

ტექსტი, რომელიც გაეგზავნება ჩვენს რედაქტორებს:

თქვენი კომენტარი (სურვილისამებრ):