La valeur critique de la distribution de Fisher. Le critère exact de Fisher
À l'aide de cet exemple, nous examinerons comment la fiabilité de l'équation de régression résultante est évaluée. Le même test permet de tester l'hypothèse selon laquelle les coefficients de régression sont simultanément égaux à zéro, a=0, b=0. En d’autres termes, l’essence des calculs est de répondre à la question : peut-il être utilisé pour des analyses et des prévisions plus approfondies ?
Pour déterminer si les variances dans deux échantillons sont similaires ou différentes, utilisez ce test t.
Ainsi, le but de l'analyse est d'obtenir une estimation, à l'aide de laquelle on pourrait affirmer qu'à un certain niveau de α, l'équation de régression résultante est statistiquement fiable. Pour ça le coefficient de détermination R 2 est utilisé.
Le test de la signification d'un modèle de régression est effectué à l'aide du test F de Fisher, dont la valeur calculée est le rapport entre la variance de la série originale d'observations de l'indicateur étudié et l'estimation non biaisée de la variance de la séquence résiduelle. pour ce modèle.
Si la valeur calculée avec k 1 =(m) et k 2 =(n-m-1) degrés de liberté est supérieure à la valeur tabulée à un niveau de signification donné, alors le modèle est considéré comme significatif.
où m est le nombre de facteurs dans le modèle.
La signification statistique de la régression linéaire appariée est évaluée à l'aide de l'algorithme suivant :
1. Une hypothèse nulle est émise selon laquelle l'équation dans son ensemble est statistiquement non significative : H 0 : R 2 =0 au niveau de signification α.
2. Ensuite, déterminez la valeur réelle du critère F : ![]()
![]()
où m=1 pour la régression par paires.
3. La valeur tabulée est déterminée à partir des tableaux de distribution de Fisher pour un niveau de signification donné, en tenant compte du fait que le nombre de degrés de liberté pour la somme totale des carrés (variance plus grande) est de 1 et le nombre de degrés de liberté pour le résidu la somme des carrés (variance plus petite) en régression linéaire est n-2 (ou via la fonction Excel FRIST(probability,1,n-2)).
Le tableau F est la valeur maximale possible du critère sous l'influence de facteurs aléatoires avec des degrés de liberté et un niveau de signification α donnés. Le niveau de signification α est la probabilité de rejeter l’hypothèse correcte, à condition qu’elle soit vraie. Généralement, α est considéré comme étant égal à 0,05 ou 0,01.
4. Si la valeur réelle du test F est inférieure à la valeur du tableau, alors ils disent qu'il n'y a aucune raison de rejeter l'hypothèse nulle.
Dans le cas contraire, l’hypothèse nulle est rejetée et l’hypothèse alternative sur la signification statistique de l’équation dans son ensemble est acceptée avec probabilité (1-α).
Valeur du tableau du critère avec degrés de liberté k 1 =1 et k 2 =48, F tableau = 4
Conclusions: Puisque la valeur réelle F > F tableau, le coefficient de détermination est statistiquement significatif ( l'estimation de l'équation de régression trouvée est statistiquement fiable) .
Analyse de variance
.Indicateurs de qualité des équations de régression
Exemple. Sur la base d'un total de 25 entreprises commerciales, la relation entre les caractéristiques suivantes est étudiée : X - prix du produit A, en milliers de roubles ; Y est le bénéfice d'une entreprise commerciale, en millions de roubles. Lors de l'évaluation du modèle de régression, les résultats intermédiaires suivants ont été obtenus : ∑(y i -y x) 2 = 46 000 ; ∑(y i -y moy) 2 = 138 000. Quel indicateur de corrélation peut-on déterminer à partir de ces données ? Calculer la valeur de cet indicateur en fonction de ce résultat et en utilisant Test F de Fisher tirer des conclusions sur la qualité du modèle de régression.
Solution. A partir de ces données, nous pouvons déterminer le rapport de corrélation empirique :  , où ∑(y moy -y x) 2 = ∑(y i -y moy) 2 - ∑(y i -y x) 2 = 138 000 - 46 000 = 92 000.
, où ∑(y moy -y x) 2 = ∑(y i -y moy) 2 - ∑(y i -y x) 2 = 138 000 - 46 000 = 92 000.
η 2 = 92 000/138 000 = 0,67, η = 0,816 (0,7< η < 0.9 - связь между X и Y высокая).
Test F de Fisher: n = 25, m = 1.
R 2 = 1 - 46 000/138 000 = 0,67, F = 0,67/(1-0,67)x(25 - 1 - 1) = 46. Tableau F (1 ; 23) = 4,27
Puisque la valeur réelle F > Ftable, l'estimation trouvée de l'équation de régression est statistiquement fiable.
Question : Quelles statistiques sont utilisées pour tester la signification d'un modèle de régression ?
Réponse : Pour la signification de l'ensemble du modèle, les statistiques F (test de Fisher) sont utilisées.
But. Tester l'hypothèse selon laquelle deux variances appartiennent à la même population générale et donc leur égalité.
Hypothèse nulle. S 2 2 = S 1 2
Hypothèse alternative. Il existe les options suivantes pour N A, selon les zones critiques qui diffèrent :
1. S 1 2 > S 2 2 . L'option la plus couramment utilisée est H A. La région critique est la queue supérieure de la distribution F.
2. S 1 2< S 2 2 . Критическая область - нижний хвост F-распределения. Ввиду частого отсутствия нижнего хвоста, в таблицах критическую область обычно сводят к варианту 1, меняя местами дисперсии.
3. Double face S 1 2 ≠S 2 2. Combinaison des deux premiers.
Conditions préalables. Les données sont indépendantes et normalement distribuées. L'hypothèse selon laquelle les variances de deux populations normales sont égales est acceptée si le rapport entre la plus grande et la plus petite variance est inférieur à la valeur critique de la distribution de Fisher.
F P = S 1 2 /S 2 2
Note. Avec la méthode de vérification décrite, la valeur de Fpasch doit nécessairement être supérieure à un. Le critère est sensible à la violation de l’hypothèse de normalité.
Pour une alternative bilatérale S 1 2 ≠S 2 2 l'hypothèse nulle est acceptée si la condition est remplie :
F l - α /2< Fрасч < F α /2
Exemple
Les paramètres thermophysiques ont été déterminés à l'aide d'une méthode thermométrique complexe. caractéristiques (TFC) du malt vert. Pour préparer les échantillons, nous avons prélevé du malt vieilli quatre jours sec à l'air (humidité moyenne W=19 %) et humide (W=45 %) conformément à la nouvelle technologie de préparation du malt caramel. Des expériences ont montré que la conductivité thermique λ du malt humide est environ 2,5 fois supérieure à celle du malt sec et que la capacité thermique volumétrique ne dépend pas clairement de la teneur en humidité du malt. Par conséquent, à l'aide du test F, nous avons vérifié la possibilité de généraliser les données basées sur des valeurs moyennes sans prendre en compte l'humidité.
Les données calculées sont résumées dans le tableau 5.1
Tableau 5.1
Données pour le calcul du critère F
Une valeur de dispersion plus grande a été obtenue pour W=45%, c'est-à-dire S 2 45 = S 1 2 , S 2 19 = S 2 2 et F P = S 1 2 /S 2 2 =1,35. À partir du tableau 5.2 pour le degré de liberté f 1 =N 1 -1=5 f 2 =N 2 -1=4 à γ=0,95 nous déterminons F KR =6,2. L'hypothèse nulle formulée comme « Dans la gamme de teneur en humidité du malt vert de 19 à 45 %, son influence sur la capacité thermique volumétrique peut être négligée » ou « S 2 45 = S 2 19 » avec une probabilité de confiance de 95 % a été confirmée. , puisque Fp Un exemple de test d'une hypothèse sur l'appartenance de deux variances à la même population en utilisant le critère de Fisher sous Excel Les données sont présentées pour deux échantillons indépendants (tableau 5.2) du degré d'absorption d'eau des grains de blé. Une étude des effets des champs magnétiques à basse fréquence a été menée. Tableau 5.2 Résultats de la recherche Avant de tester l’hypothèse d’égalité des moyennes de ces échantillons, il est nécessaire de tester l’hypothèse d’égalité des variances afin de savoir quel critère choisir pour la tester. Sur la fig. 5.1 montre un exemple de test de l'hypothèse selon laquelle deux variances appartiennent à la même population en utilisant le critère de Fisher à l'aide du logiciel Microsoft Excel. Figure 5.1 Exemple de test d'appartenance de deux variances à une même population en utilisant le critère de Fisher Les données sources se trouvent dans les cellules situées à l'intersection des colonnes C et D avec les lignes 3 à 10. Faisons ce qui suit : 1. Déterminons si la loi de distribution des premier et deuxième échantillons peut être considérée comme normale (colonnes C et D, respectivement). Sinon (pour au moins un échantillon), alors il faut utiliser un test non paramétrique si oui, on continue ; 2. Calculez les écarts pour les première et deuxième colonnes. Pour ce faire, dans les cellules SP et D11 nous plaçons respectivement les fonctions =DISP(SZ:C10) et =DISP(DЗ:D10). Le résultat de ces fonctions est la valeur de variance calculée pour chaque colonne, respectivement. 3. Trouvez la valeur calculée pour le critère de Fisher. Pour ce faire, vous devez diviser la plus grande variance par la plus petite. Dans la cellule F13, nous plaçons la formule =C11/D11, qui effectue cette opération. 4. Déterminer si l'hypothèse d'égalité des variances peut être acceptée. Il existe deux méthodes, présentées dans l'exemple. Selon la première méthode, en fixant un niveau de signification, par exemple 0,05, on calcule la valeur critique de la distribution de Fisher pour cette valeur et le nombre de degrés de liberté correspondant. Dans la cellule F14, entrez la fonction =FPACPOBP(0,05;7;7) (où 0,05 est le niveau de signification spécifié ; 7 est le nombre de degrés de liberté du numérateur et 7 (seconde) est le nombre de degrés de liberté de le dénominateur). Le nombre de degrés de liberté est égal au nombre d’expériences moins un. Le résultat est 3,787051. Puisque cette valeur est supérieure à la valeur calculée de 1,81144, il faut accepter l'hypothèse nulle d'égalité des variances. Selon la deuxième option, la probabilité correspondante est calculée pour la valeur calculée obtenue du critère de Fisher. Pour ce faire, entrez la fonction =FPACP(F13,7,7) dans la cellule F15. Puisque la valeur résultante de 0,22566 est supérieure à 0,05, l'hypothèse d'égalité des variances est acceptée. Cela peut être fait par une fonction spéciale. Sélectionner les éléments de menu de manière séquentielle Service
, Analyse des données
. La fenêtre suivante apparaîtra (Fig. 5.2). Figure 5.2 Fenêtre de sélection de la méthode de traitement Dans cette fenêtre sélectionnez " F-mecm à deux échantillons pour les écarts
" En conséquence, une fenêtre apparaîtra comme le montre la Fig. 5.3. Ici, vous définissez les intervalles (numéros de cellules) des première et deuxième variables, le niveau de signification (alpha) et l'endroit où le résultat sera trouvé. Définissez tous les paramètres nécessaires et cliquez sur OK. Le résultat du travail est présenté sur la Fig. 5.4 Il convient de noter que la fonction teste un critère unilatéral et le fait correctement. Dans le cas où la valeur du critère est supérieure à 1, la valeur critique supérieure est calculée. Figure 5.3 Fenêtre de paramétrage Lorsque la valeur du critère est inférieure à 1, la valeur critique inférieure est calculée. Nous vous rappelons que l'hypothèse d'égalité des variances est rejetée si la valeur du critère est supérieure à la valeur critique supérieure ou inférieure à la valeur critique inférieure. Figure 5.4 Test d'égalité des variances La fonction FISCHER renvoie la transformée de Fisher des arguments en X . Cette transformation produit une fonction qui a une distribution normale plutôt que asymétrique. La fonction FISCHER est utilisée pour tester l'hypothèse à l'aide du coefficient de corrélation. Lorsque vous travaillez avec cette fonction, vous devez définir la valeur de la variable. Il convient de noter d’emblée qu’il existe certaines situations dans lesquelles cette fonction ne produira aucun résultat. Ceci est possible si la variable : L'équation utilisée pour décrire mathématiquement la fonction FISCHER est la suivante : Z"=1/2*ln(1+x)/(1-x) Regardons l'utilisation de cette fonction à l'aide de 3 exemples spécifiques. Exemple 1. À l'aide de données sur l'activité des organisations commerciales, il est nécessaire d'évaluer la relation entre le profit Y (millions de roubles) et les coûts X (millions de roubles) utilisés pour le développement de produits (indiqués dans le tableau 1). Tableau 1 – Données initiales : Le schéma pour résoudre de tels problèmes est le suivant : Les résultats de la résolution de ce problème avec les fonctions utilisées dans Excel sont présentés dans la figure 1. Figure 1 – Exemple de calculs. Ainsi, avec une probabilité de 0,95, le coefficient de corrélation linéaire est compris entre (–0,386) et (–0,990) avec une erreur type de 0,205. Exemple 2. Vérifiez la signification statistique de l'équation de régression multiple à l'aide du test F de Fisher et tirez des conclusions. Pour vérifier la significativité de l'équation dans son ensemble, nous émettons l'hypothèse H 0 sur l'insignifiance statistique du coefficient de détermination et l'hypothèse inverse H 1 sur la signification statistique du coefficient de détermination : H 1 : R 2 ≠ 0. Testons les hypothèses à l'aide du test F de Fisher. Les indicateurs sont présentés dans le tableau 2. Tableau 2 - Données initiales Pour ce faire, nous utilisons la fonction dans Excel : PLUS RAPIDE (α;p;n-p-1) Sachant que α = 0,05, p = 2 et n = 53, on obtient la valeur suivante pour F crit (voir Figure 2). Figure 2 – Exemple de calculs. On peut donc dire que F calculé > F critique. En conséquence, l'hypothèse H 1 sur la signification statistique du coefficient de détermination est acceptée. Exemple 3. Utilisation des données de 23 entreprises sur : X est le prix du produit A, en milliers de roubles ; Y est le bénéfice d'une entreprise commerciale, en millions de roubles ; leur dépendance est à l'étude. Le modèle de régression a été estimé comme suit : ∑(yi-yx) 2 = 50 000 ; ∑(yi-yср) 2 = 130000. Quel indicateur de corrélation peut-on déterminer à partir de ces données ? Calculez la valeur de l'indicateur de corrélation et, à l'aide du critère de Fisher, tirez une conclusion sur la qualité du modèle de régression. Déterminons F crit à partir de l'expression : F calculé = R 2 /23*(1-R 2) où R est le coefficient de détermination égal à 0,67. Ainsi, la valeur calculée F calc = 46. Pour déterminer F crit, nous utilisons la distribution de Fisher (voir Figure 3). Figure 3 – Exemple de calculs. Ainsi, l’estimation résultante de l’équation de régression est fiable. Le test exact de Fisher est un critère utilisé pour comparer deux indicateurs relatifs qui caractérisent la fréquence d'une caractéristique particulière qui a deux valeurs. Les données initiales permettant de calculer le test exact de Fisher sont généralement regroupées sous la forme d'un tableau à quatre champs. Le critère a été proposé pour la première fois Ronald Fisher dans son livre Conception d'expériences. Cela s'est produit en 1935. Fischer lui-même a affirmé que Muriel Bristol l'avait incité à cette idée. Au début des années 1920, Ronald, Muriel et William Roach étaient en poste en Angleterre dans une station expérimentale agricole. Muriel affirmait qu'elle pouvait déterminer l'ordre dans lequel le thé et le lait étaient versés dans sa tasse. A cette époque, il n’était pas possible de vérifier l’exactitude de sa déclaration. Cela a donné naissance à l'idée de Fisher de « l'hypothèse nulle ». Le but n’était pas de prouver que Muriel pouvait faire la différence entre des tasses de thé préparées différemment. Il a été décidé de réfuter l'hypothèse selon laquelle une femme fait un choix au hasard. Il a été déterminé que l’hypothèse nulle ne pouvait être ni prouvée ni justifiée. Mais cela peut être réfuté lors d’expérimentations. 8 tasses ont été préparées. Les quatre premiers sont d'abord remplis de lait, les quatre autres de thé. Les tasses étaient mélangées. Bristol a proposé de goûter le thé et de diviser les tasses selon la méthode de préparation du thé. Le résultat aurait dû être deux groupes. L'histoire dit que l'expérience a été un succès. Grâce au test de Fisher, la probabilité que Bristol agisse intuitivement a été réduite à 0,01428. C'est-à-dire qu'il a été possible d'identifier correctement la coupe dans un cas sur 70. Mais il n'y a toujours aucun moyen de réduire à zéro les chances que Madame détermine par hasard. Même si vous augmentez le nombre de tasses. Cette histoire a donné une impulsion au développement de « l’hypothèse nulle ». Dans le même temps, le critère exact de Fisher a été proposé, dont l'essence est d'énumérer toutes les combinaisons possibles de variables dépendantes et indépendantes. Le test exact de Fisher est principalement utilisé à des fins de comparaison petits échantillons. Il y a deux bonnes raisons à cela. Premièrement, le calcul du critère est assez lourd et peut prendre beaucoup de temps ou nécessiter des ressources informatiques puissantes. Deuxièmement, le critère est assez précis (ce qui se reflète même dans son nom), ce qui lui permet d'être utilisé dans des études avec un petit nombre d'observations. Une place particulière est accordée au test exact de Fisher en médecine. Il s’agit d’une méthode importante de traitement des données médicales qui a trouvé son application dans de nombreuses études scientifiques. Grâce à lui, il est possible d'étudier la relation entre certains facteurs et résultats, de comparer la fréquence des états pathologiques entre deux groupes de sujets, etc. Un analogue du test exact de Fisher est le test du Chi carré de Pearson, tandis que le test exact de Fisher a une puissance plus élevée, en particulier lors de la comparaison de petits échantillons, et présente donc un avantage dans ce cas. Disons que nous étudions la dépendance de la fréquence des naissances d'enfants atteints de malformations congénitales (CDD) au tabagisme maternel pendant la grossesse. Pour cela, deux groupes de femmes enceintes ont été sélectionnés, l'un étant un groupe expérimental composé de 80 femmes ayant fumé au cours du premier trimestre de la grossesse, et le second étant un groupe témoin comprenant 90 femmes menant un mode de vie sain tout au long de la grossesse. Le nombre de cas de malformation congénitale fœtale déterminés par échographie dans le groupe expérimental était de 10, dans le groupe de comparaison - 2. Nous composons d’abord tableau de contingence à quatre champs: Le test exact de Fisher est calculé à l'aide de la formule suivante : où N est le nombre total de sujets répartis en deux groupes ; ! - factorielle, qui est le produit d'un nombre et d'une suite de nombres dont chacun est inférieur au précédent de 1 (par exemple, 4 ! = 4 3 2 1) À la suite des calculs, nous constatons que P = 0,0137. L'avantage de la méthode est que le critère résultant correspond à la valeur exacte du niveau de signification p. Autrement dit, la valeur de 0,0137 obtenue dans notre exemple est le niveau de signification des différences entre les groupes comparés en termes de fréquence des malformations congénitales fœtales. Il suffit de comparer ce nombre avec le niveau de signification critique, généralement pris en recherche médicale à 0,05. Dans notre exemple P< 0,05, в связи с чем делаем вывод о наличии прямой взаимосвязи курения и вероятности развития ВПР плода. Частота возникновения врожденной патологии у детей курящих женщин statistiquement significativement plus élevé que les non-fumeurs. Renvoie l'inverse de la distribution de probabilité F (à droite). Si p = FRIST(x;...), alors FRIST(p;...) = x. La distribution F peut être utilisée dans un test F, qui compare le degré de dispersion de deux ensembles de données. Par exemple, vous pouvez analyser la répartition des revenus aux États-Unis et au Canada pour déterminer si les deux pays sont similaires en termes de densité de revenus. Important: Cette fonctionnalité a été remplacée par une ou plusieurs nouvelles fonctionnalités offrant une plus grande précision et portant des noms qui reflètent mieux leur objectif. Bien que cette fonctionnalité soit toujours utilisée à des fins de compatibilité descendante, elle pourrait ne plus être disponible dans les futures versions d'Excel. Nous vous recommandons donc d'utiliser les nouvelles fonctionnalités. Pour en savoir plus sur les nouvelles fonctions, consultez les articles Fonction F.REV et Fonction F.REV.PH. FRIST(probabilité,degrés_liberté1,degrés_liberté2) Les arguments de la fonction FALTER sont décrits ci-dessous. Probabilité- argument requis. Probabilité associée à la distribution F cumulative. Degrés_de_liberté1- argument requis. Numérateur de degrés de liberté. Degrés_de_liberté2- argument requis. Dénominateur des degrés de liberté. Si l'un des arguments n'est pas un nombre, FRATE renvoie la valeur d'erreur #VALUE ! Si « probabilité »< 0 или "вероятность" >1, la fonction FRIST renvoie la valeur d'erreur #NUM!. Si la valeur de Degrees_freedom1 ou Degrees_freedom2 n'est pas un nombre entier, elle est tronquée. Si "degrés_liberté1"< 1 или "степени_свободы1" ≥ 10^10, функция FРАСПОБР возвращает значение ошибки #ЧИСЛО!. Si "degrés_liberté2"< 1 или "степени_свободы2" ≥ 10^10, функция FРАСПОБР возвращает значение ошибки #ЧИСЛО!. La fonction FDIST peut être utilisée pour déterminer les valeurs critiques de la distribution F. Par exemple, les résultats de l'ANOVA incluent généralement des données pour la statistique F, la probabilité F et la valeur critique de la distribution F à un niveau de signification de 0,05. Pour déterminer la valeur critique de F, vous devez utiliser le niveau de signification comme argument de probabilité de la fonction FDIST. Étant donné une valeur de probabilité, la fonction FDIST recherche une valeur de x pour laquelle FDIST(x,degrees_of_freedom1,degrees_of_freedom2) = probabilité. Ainsi, la précision de la fonction FDIST dépend de la précision de FDIST. Pour rechercher, la fonction FRIST utilise une méthode d'itération. Si la recherche ne se termine pas après 100 itérations, la valeur d'erreur #N/A est renvoyée. Copiez les exemples de données du tableau suivant et collez-les dans la cellule A1 d'une nouvelle feuille de calcul Excel. Pour afficher les résultats des formules, sélectionnez-les et appuyez sur F2, puis appuyez sur Entrée. Si nécessaire, modifiez la largeur des colonnes pour voir toutes les données.Nombre Numéro d'échantillon
expérience
2 ,
0,027
0,075
0,036
0,4
0,1
0,08
0,12
0,105
0,32
0,075
0,45
0,12
0,049
0,06
0,105
0,075




Description de la fonction FISCHER dans Excel
Estimation de la relation entre profit et coûts à l'aide de la fonction FISHER
№
X Oui
1
210 000 000,00 RUR 95 000 000,00 RUR
2
1 068 000 000,00 RUB 76 000 000,00 RUR
3
1 005 000 000,00 RUB 78 000 000,00 RUR
4
610 000 000,00 RUR 89 000 000,00 RUR
5
768 000 000,00 RUR 77 000 000,00 RUR
6
799 000 000,00 RUR 85 000 000,00 RUR
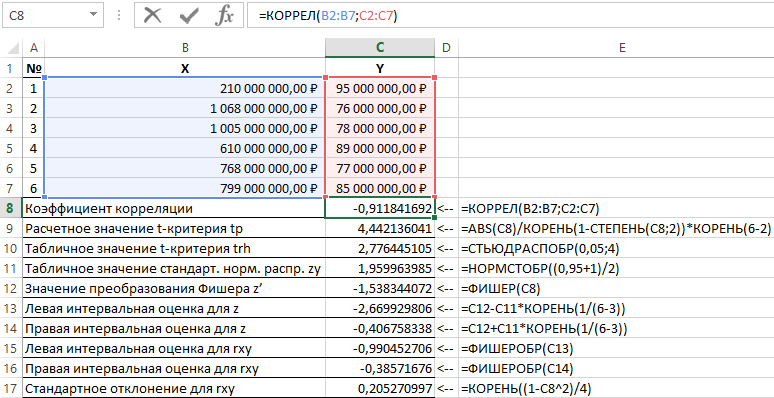
Non. Nom de l'indicateur Formule de calcul
1
Coefficient de corrélation =CORREL(B2:B7,C2:C7)
2
Valeur de test t calculée tp =ABS(C8)/SQRT(1-PUISSANCE(C8,2))*SQRT(6-2)
3
Valeur du tableau du test t trh =ETUDICOUVERTURE(0.05,4)
4
Valeur du tableau de la distribution normale standard zy =NORMSINV((0.95+1)/2)
5
Valeur de transformation de Fisher z =PÊCHEUR(C8)
6
Estimation de l'intervalle gauche pour z =C12-C11*RACINE(1/(6-3))
7
Estimation de l'intervalle droit pour z =C12+C11*RACINE(1/(6-3))
8
Estimation de l'intervalle gauche pour rxy =PÊCHEURBR(C13)
9
Estimation de l'intervalle droit pour rxy =PÊCHEURBR(C14)
10
Écart type pour rxy =RACINE((1-C8^2)/4)
Vérification de la signification statistique de la régression à l'aide de la fonction PLUS RAPIDE

Calcul de la valeur de l'indicateur de corrélation dans Excel

1. Historique de l'évolution du critère
2. À quoi sert le test exact de Fisher ?
3. Dans quels cas le test exact de Fisher peut-il être utilisé ?
Un test bilatéral évalue les différences de fréquence dans deux directions. C'est-à-dire que la probabilité d'une fréquence à la fois plus élevée et plus faible du phénomène dans le groupe expérimental par rapport au groupe témoin est évaluée.4. Comment calculer le test exact de Fisher ?
5. Comment interpréter la valeur du test exact de Fisher ?
Syntaxe
Remarques
Exemple
