Συνθήκη Fano για την κατασκευή βέλτιστου κώδικα. Κατάσταση Fano. Πρακτική εφαρμογή της συνθήκης Fano

Διάλεξη 3. Γενικά θεωρήματαΗχεία

Δυναμική ενός συστήματος υλικών σημείωναποτελεί σημαντικό κλάδο της θεωρητικής μηχανικής. Εδώ εξετάζουμε κυρίως προβλήματα σχετικά με την κίνηση μηχανικών συστημάτων (συστήματα υλικών σημείων) με πεπερασμένο αριθμό βαθμών ελευθερίας - μέγιστος αριθμόςανεξάρτητες παράμετροι που καθορίζουν τη θέση του συστήματος. το κύριο καθήκονδυναμική συστήματος – μελέτη των νόμων της κίνησης στερεόςκαι μηχανικά συστήματα.

Η απλούστερη προσέγγιση για τη μελέτη της κίνησης ενός συστήματος, που αποτελείται από Νυλικά σημεία, καταλήγει στην εξέταση των κινήσεων κάθε μεμονωμένου σημείου του συστήματος. Σε αυτή την περίπτωση, όλες οι δυνάμεις που δρουν σε κάθε σημείο του συστήματος, συμπεριλαμβανομένων των δυνάμεων αλληλεπίδρασης μεταξύ σημείων, πρέπει να προσδιοριστούν.

Καθορίζοντας την επιτάχυνση κάθε σημείου σύμφωνα με τον δεύτερο νόμο του Νεύτωνα (1.2), λαμβάνουμε για κάθε σημείο τρεις βαθμωτούς διαφορικούς νόμους κίνησης δεύτερης τάξης, δηλ. 3 Ν διαφορικούς νόμους κίνησης για ολόκληρο το σύστημα.

Για να βρεθούν οι εξισώσεις κίνησης ενός μηχανικού συστήματος με βάση δεδομένες δυνάμεις και αρχικές συνθήκες για κάθε σημείο του συστήματος, πρέπει να ενσωματωθούν οι διαφορικοί νόμοι που προκύπτουν. Αυτό το πρόβλημα είναι δύσκολο ακόμη και στην περίπτωση δύο υλικών σημείων που κινούνται μόνο υπό την επίδραση δυνάμεων αλληλεπίδρασης σύμφωνα με το νόμο της καθολικής έλξης (πρόβλημα δύο σωμάτων) και εξαιρετικά δύσκολο στην περίπτωση τριών σημείων αλληλεπίδρασης (πρόβλημα τριών σωμάτων ).

Επομένως, είναι απαραίτητο να βρεθούν μέθοδοι για την επίλυση προβλημάτων που θα οδηγούσαν σε επιλύσιμες εξισώσεις και θα έδιναν μια ιδέα της κίνησης ενός μηχανικού συστήματος. Τα γενικά θεωρήματα της δυναμικής, ως συνέπεια των διαφορικών νόμων της κίνησης, μας επιτρέπουν να αποφύγουμε την πολυπλοκότητα που προκύπτει κατά την ολοκλήρωση και να επιτύχουμε τα απαραίτητα αποτελέσματα.

3. 1. Γενικές σημειώσεις

Θα αριθμήσουμε τα σημεία του μηχανικού συστήματος με δείκτες Εγώ, ι, κκ.λπ., που διατρέχουν όλες τις τιμές 1, 2, 3… Ν, Οπου Ν – αριθμός σημείων του συστήματος. Φυσικές ποσότητεςπου σχετίζονται με κτο σημείο ορίζεται από τον ίδιο δείκτη με το σημείο. Για παράδειγμα, εκφράστε το διάνυσμα ακτίνας και την ταχύτητα, αντίστοιχα κτο σημείο.

Σε κάθε σημείο του συστήματος επιδρούν δυνάμεις δύο προέλευσης: πρώτον, δυνάμεις των οποίων οι πηγές βρίσκονται έξω από το σύστημα, που ονομάζονται εξωτερικόςδυνάμεις και ορίζονται ; δεύτερον, δυνάμεις από άλλα σημεία ενός δεδομένου συστήματος, που καλούνται εσωτερικόςδυνάμεις και ορίζονται . Οι εσωτερικές δυνάμεις ικανοποιούν τον τρίτο νόμο του Νεύτωνα. Ας εξετάσουμε τις απλούστερες ιδιότητες των εσωτερικών δυνάμεων που δρουν σε ολόκληρο το μηχανικό σύστημα σε οποιαδήποτε κατάσταση.

Πρώτη ιδιοκτησία. Το γεωμετρικό άθροισμα όλων των εσωτερικών δυνάμεων του συστήματος (το κύριο διάνυσμα των εσωτερικών δυνάμεων) είναι ίσο με μηδέν.

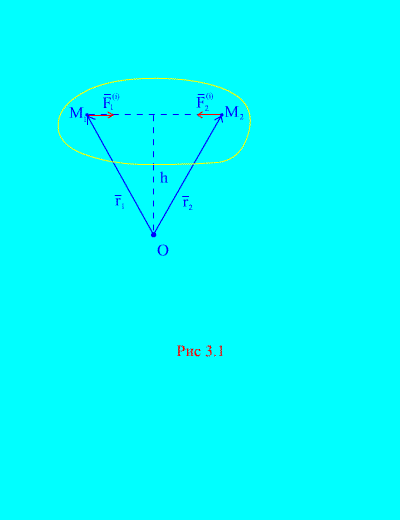
Πράγματι, αν λάβουμε υπόψη οποιαδήποτε δύο αυθαίρετα σημεία του συστήματος, για παράδειγμα και (Εικ. 3.1), τότε για αυτούς , επειδή Οι δυνάμεις δράσης και αντίδρασης είναι πάντα ίσες σε μέγεθος, ενεργώντας κατά μήκος μιας γραμμής δράσης προς την αντίθετη κατεύθυνση, η οποία συνδέει τα σημεία αλληλεπίδρασης. Επομένως, το κύριο διάνυσμα των εσωτερικών δυνάμεων αποτελείται από ζεύγη δυνάμεων αλληλεπιδρώντων σημείων

(3.1)

Δεύτερη ιδιοκτησία. Το γεωμετρικό άθροισμα των ροπών όλων των εσωτερικών δυνάμεων σε σχέση με ένα αυθαίρετο σημείο του χώρου είναι ίσο με μηδέν.

Ας εξετάσουμε ένα σύστημα ροπών δυνάμεων και σε σχέση με το σημείο ΣΧΕΤΙΚΑ ΜΕ(Εικ. 3.1). Από (Εικ. 3.1). είναι ξεκάθαρο ότι

,

επειδή και οι δύο δυνάμεις έχουν τους ίδιους βραχίονες και αντίθετες κατευθύνσεις διανυσματικών ροπών. Κύριο σημείοεσωτερικές δυνάμεις σε σχέση με ένα σημείο ΣΧΕΤΙΚΑ ΜΕαποτελείται από το διανυσματικό άθροισμα τέτοιων παραστάσεων και ίσο με μηδέν. Ως εκ τούτου,

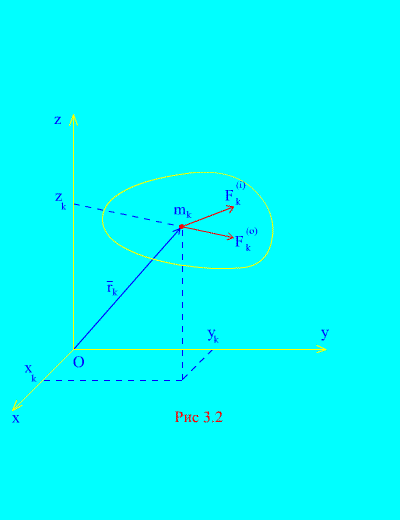
Αφήστε τις εξωτερικές και εσωτερικές δυνάμεις που δρουν σε ένα μηχανικό σύστημα που αποτελείται από Νσημεία (Εικ. 3.2). Εάν το αποτέλεσμα των εξωτερικών δυνάμεων και το αποτέλεσμα όλων των εσωτερικών δυνάμεων εφαρμόζεται σε κάθε σημείο του συστήματος, τότε για οποιοδήποτε κ- σημεία του συστήματος μπορούν να συντίθενται διαφορικές εξισώσειςκινήσεις. Θα υπάρχουν συνολικά τέτοιες εξισώσεις Ν:

και σε προβολές σε σταθερούς άξονες συντεταγμένων 3 Ν:

(3.4)

Οι διανυσματικές εξισώσεις (3.3) ή οι ισοδύναμες βαθμωτές εξισώσεις (3.4) αντιπροσωπεύουν τους διαφορικούς νόμους κίνησης των υλικών σημείων ολόκληρου του συστήματος. Εάν όλα τα σημεία κινούνται παράλληλα σε ένα επίπεδο ή μια ευθεία γραμμή, τότε ο αριθμός των εξισώσεων (3.4) στην πρώτη περίπτωση θα είναι 2 Ν, στο δεύτερο Ν.

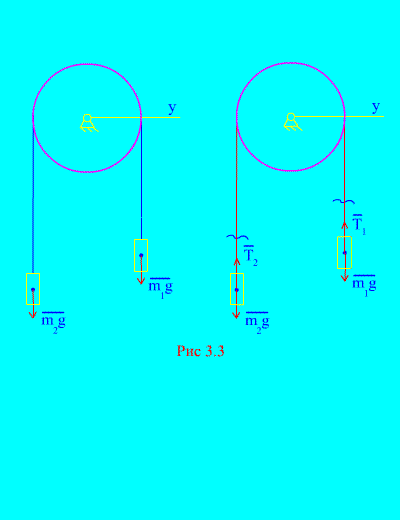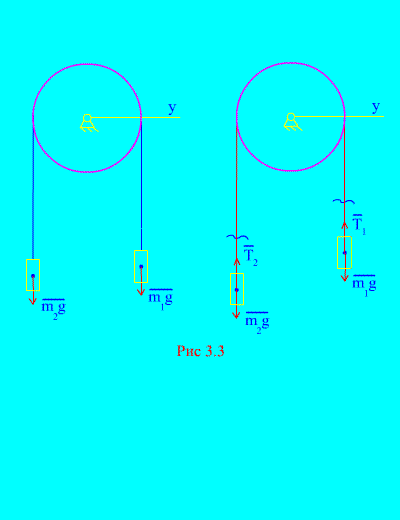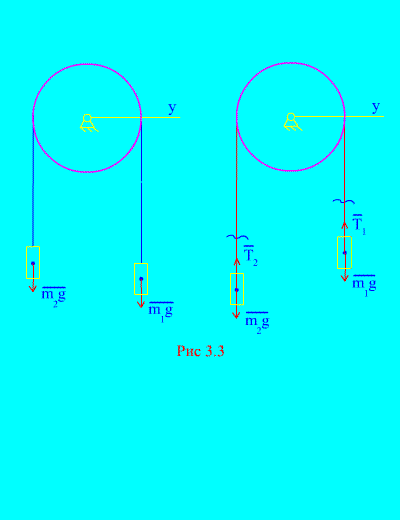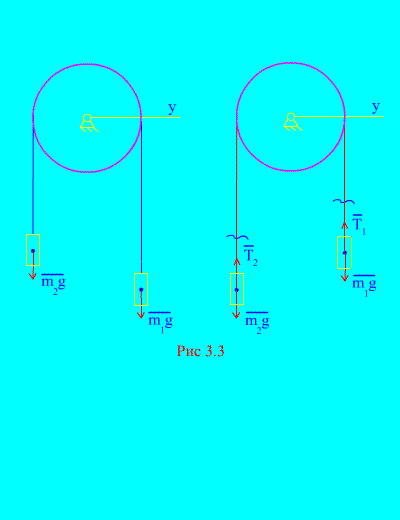
Παράδειγμα 1.Δύο μάζες συνδέονται μεταξύ τους με ένα μη εκτάσιμο καλώδιο που ρίχνεται πάνω από ένα μπλοκ (Εικ. 3.3). Η παραμέληση των δυνάμεων τριβής, καθώς και η μάζα του μπλοκ και του καλωδίου, καθορίζουν το νόμο της κίνησης των φορτίων και την τάση του καλωδίου.

Λύση. Το σύστημα αποτελείται από δύο υλικά σώματα (που συνδέονται με ένα μη εκτατό καλώδιο) που κινούνται παράλληλα στον ίδιο άξονα Χ.Ας γράψουμε τους διαφορικούς νόμους της κίνησης σε προβολές στον άξονα Χγια όλους.

Αφήστε το σωστό βάρος να πέσει με την επιτάχυνση, τότε το αριστερό βάρος θα αυξηθεί με την επιτάχυνση. Απελευθερωνόμαστε ψυχικά από τη σύνδεση (καλώδιο) και την αντικαθιστούμε με αντιδράσεις και (Εικ. 3.3). Θεωρώντας τα σώματα ελεύθερα, ας συντάξουμε τους διαφορικούς νόμους της κίνησης σε προβολή στον άξονα Χ(που σημαίνει ότι οι τάσεις του νήματος είναι εσωτερικές δυνάμεις και το βάρος των φορτίων είναι εξωτερικά):

Δεδομένου ότι και (τα σώματα συνδέονται με ένα μη εκτατό καλώδιο), λαμβάνουμε

Επίλυση αυτών των εξισώσεων για την επιτάχυνση και την τάση του καλωδίου Τ, παίρνουμε

.

Σημειώστε ότι η τάση στο καλώδιο δεν είναι ίση με τη δύναμη βαρύτητας του αντίστοιχου φορτίου.

3. 2. Θεώρημα για την κίνηση του κέντρου μάζας

Είναι γνωστό ότι ένα άκαμπτο σώμα και ένα μηχανικό σύστημα σε ένα επίπεδο μπορούν να κινούνται αρκετά περίπλοκα. Το πρώτο θεώρημα για την κίνηση ενός σώματος και ενός μηχανικού συστήματος μπορεί να επιτευχθεί ως εξής: ρίξτε ένα k.-l. ένα αντικείμενο που αποτελείται από πολλά στερεά σώματα στερεωμένα μεταξύ τους. Είναι ξεκάθαρο ότι θα πετάξει σε παραβολή. Αυτό αποκαλύφθηκε κατά τη μελέτη της κίνησης του σημείου. Ωστόσο, τώρα το αντικείμενο δεν είναι ένα σημείο. Γυρίζει και ταλαντεύεται κατά τη διάρκεια της πτήσης του γύρω από κάποιο αποτελεσματικό κέντρο που κινείται σε παραβολή. Το πρώτο θεώρημα για την κίνηση σύνθετων αντικειμένων λέει ότι ένα συγκεκριμένο ενεργό κέντρο είναι το κέντρο μάζας ενός κινούμενου αντικειμένου. Το κέντρο μάζας δεν βρίσκεται απαραίτητα στο ίδιο το σώμα, μπορεί να βρίσκεται κάπου έξω από αυτό.

Θεώρημα. Το κέντρο μάζας ενός μηχανικού συστήματος κινείται ως υλικό σημείο με μάζα ίση με τη μάζα ολόκληρου του συστήματος, στο οποίο ασκούνται όλες οι εξωτερικές δυνάμεις που δρουν στο σύστημα.

Για να αποδείξουμε το θεώρημα, ξαναγράφουμε τους διαφορικούς νόμους της κίνησης (3.3) σε την παρακάτω φόρμα:

(3.5)

Οπου Ν – αριθμός σημείων του συστήματος.

Ας προσθέσουμε τις εξισώσεις μαζί ανά όρο:

(ΕΝΑ)

Η θέση του κέντρου μάζας του μηχανικού συστήματος σε σχέση με το επιλεγμένο σύστημα συντεταγμένων προσδιορίζεται από τον τύπο (2.1): Οπου Μ– μάζα του συστήματος. Επειτα αριστερή πλευράισότητα (α) θα γραφεί

Το πρώτο άθροισμα στη δεξιά πλευρά της ισότητας (α) είναι ίσο με το κύριο διάνυσμα των εξωτερικών δυνάμεων και το τελευταίο, με την ιδιότητα των εσωτερικών δυνάμεων, είναι ίσο με μηδέν. Στη συνέχεια, η ισότητα (α), λαμβάνοντας υπόψη το (β), θα ξαναγραφεί

, (3.6)

εκείνοι. το γινόμενο της μάζας του συστήματος και της επιτάχυνσης του κέντρου της μάζας του είναι ίσο με το γεωμετρικό άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα.

Από την εξίσωση (3.6) προκύπτει ότι οι εσωτερικές δυνάμεις δεν επηρεάζουν άμεσα την κίνηση του κέντρου μάζας. Ωστόσο, σε ορισμένες περιπτώσεις είναι η αιτία της εμφάνισης εξωτερικών δυνάμεων που εφαρμόζονται στο σύστημα. Έτσι, οι εσωτερικές δυνάμεις που οδηγούν τους κινητήριους τροχούς ενός αυτοκινήτου σε περιστροφή προκαλούν μια εξωτερική δύναμη πρόσφυσης που ασκείται στο χείλος του τροχού να δράσει σε αυτό.

Παράδειγμα 2.Ο μηχανισμός, που βρίσκεται σε κατακόρυφο επίπεδο, είναι εγκατεστημένος σε οριζόντιο λείο επίπεδο και προσαρτάται σε αυτό με ράβδους σταθερά στερεωμένες στην επιφάνεια ΠΡΟΣ ΤΗΝΚαι μεγάλο (Εικ. 3.4).

Δίσκος 1 ακτίνας Rακίνητος. Δίσκος 2 μάζα Μκαι ακτίνα r στερεωμένο σε μανιβέλα, μήκους R+ rστο σημείο Γ 2. Ο στρόφαλος περιστρέφεται σταθερά

γωνιακή ταχύτητα. Στην αρχική στιγμή, η μανιβέλα κατέλαβε τη δεξιά οριζόντια θέση. Παραβλέποντας τη μάζα του στρόφαλου, προσδιορίστε τις μέγιστες οριζόντιες και κάθετες δυνάμεις που ασκούνται στις ράβδους εάν η συνολική μάζα του πλαισίου και του τροχού 1 είναι ίση με Μ.Εξετάστε επίσης τη συμπεριφορά του μηχανισμού απουσία ράβδων.

Λύση. Το σύστημα αποτελείται από δύο μάζες ( Ν=2 ): σταθερός δίσκος 1 με πλαίσιο και κινητός δίσκος 2. Κατευθύνετε τον άξονα στομέσω του κέντρου βάρους του ακίνητου δίσκου κατακόρυφα προς τα πάνω, άξονα Χ– κατά μήκος του οριζόντιου επιπέδου.

Ας γράψουμε το θεώρημα για την κίνηση του κέντρου μάζας (3.6) σε συντεταγμένη μορφή

Οι εξωτερικές δυνάμεις αυτού του συστήματος είναι: το βάρος του πλαισίου και του σταθερού δίσκου - Mg, κινούμενο βάρος δίσκου – mg, - η συνολική οριζόντια αντίδραση των μπουλονιών, - η κανονική ολική αντίδραση του επιπέδου. Ως εκ τούτου,

Τότε οι νόμοι της κίνησης (β) θα ξαναγραφούν

Ας υπολογίσουμε τις συντεταγμένες του κέντρου μάζας του μηχανικού συστήματος:

; (ΣΟΛ)

όπως φαίνεται από (Εικ. 3.4), , , (γωνία στροφάλου), . Αντικατάσταση αυτών των παραστάσεων στο (δ) και υπολογισμός των δεύτερων παραγώγων ως προς το χρόνο tαπό , , καταλαβαίνουμε ότι

(μι)

Αντικαθιστώντας τα (γ) και (ε) στο (β), βρίσκουμε

Η οριζόντια πίεση που ασκείται στις ράβδους είναι μεγαλύτερη και μικρότερη τιμή, Οταν cos = 1 αναλόγως, δηλ.

Η πίεση του μηχανισμού στο οριζόντιο επίπεδο έχει τις υψηλότερες και τις χαμηλότερες τιμές όταν αμαρτία αναλόγως, δηλ.

Στην πραγματικότητα, το πρώτο πρόβλημα της δυναμικής έχει λυθεί: σύμφωνα με τις γνωστές εξισώσεις κίνησης του κέντρου μάζας του συστήματος (δ), οι δυνάμεις που εμπλέκονται στην κίνηση αποκαθίστανται.

Ελλείψει ράβδων κΚαι μεγάλο (Εικ. 3.4), ο μηχανισμός μπορεί να αρχίσει να αναπηδά πάνω από το οριζόντιο επίπεδο. Αυτό θα γίνει όταν, δηλ. όταν , προκύπτει ότι η γωνιακή ταχύτητα περιστροφής του στρόφαλου, στην οποία αναπηδά ο μηχανισμός, πρέπει να ικανοποιεί την ισότητα

.

3. 3. Νόμος διατήρησης της κίνησης του κέντρου μάζας

Αν το κύριο διάνυσμα των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι ίσο με μηδέν, δηλ. , μετά από(3.6)έπεται ότι η επιτάχυνση του κέντρου μάζας είναι μηδέν, επομένως, η ταχύτητα του κέντρου μάζας είναι σταθερή ως προς το μέγεθος και την κατεύθυνση. Εάν, ειδικότερα, την αρχική στιγμή το κέντρο μάζας βρίσκεται σε ηρεμία, τότε είναι σε ηρεμία για όλη την ώρα ενώ το κύριο διάνυσμα των εξωτερικών δυνάμεων είναι ίσο με μηδέν.

Από αυτό το θεώρημα προκύπτουν αρκετά συμπεράσματα.

· Οι εσωτερικές δυνάμεις από μόνες τους δεν μπορούν να αλλάξουν τη φύση της κίνησης του κέντρου μάζας του συστήματος.

· Εάν το κύριο διάνυσμα των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι μηδέν, τότε το κέντρο μάζας βρίσκεται σε ηρεμία ή κινείται ομοιόμορφα και ευθύγραμμα.

· Εάν η προβολή του κύριου διανύσματος των εξωτερικών δυνάμεων του συστήματος σε κάποιο σταθερό άξονα είναι ίση με μηδέν, τότε η προβολή της ταχύτητας του κέντρου μάζας του συστήματος σε αυτόν τον άξονα δεν αλλάζει.

· Ένα ζεύγος δυνάμεων που ασκείται σε ένα άκαμπτο σώμα δεν μπορεί να αλλάξει την κίνηση του κέντρου μάζας του (μπορεί μόνο να προκαλέσει την περιστροφή του σώματος γύρω από το κέντρο μάζας).

Ας εξετάσουμε ένα παράδειγμα που απεικονίζει το νόμο της διατήρησης της κίνησης του κέντρου μάζας.

Παράδειγμα 3.Δύο μάζες συνδέονται με ένα μη εκτάσιμο νήμα που ρίχνεται μέσα από ένα μπλοκ (Εικ. 3.5), στερεωμένο σε σφήνα με μάζα Μ.Η σφήνα στηρίζεται σε λείο οριζόντιο επίπεδο. Την αρχική στιγμή το σύστημα ήταν σε ηρεμία. Βρείτε τη μετατόπιση της σφήνας κατά μήκος του επιπέδου όταν το πρώτο φορτίο χαμηλώσει σε ύψος Ν.Παραμελήστε τη μάζα του μπλοκ και του νήματος.

Λύση.Οι εξωτερικές δυνάμεις που δρουν στη σφήνα μαζί με τα φορτία είναι η βαρύτητα και Mg, και φυσιολογική αντίδρασηλεία οριζόντια επιφάνεια Β. Επομένως,

Δεδομένου ότι την αρχική στιγμή το σύστημα ήταν σε ηρεμία, έχουμε .

Ας υπολογίσουμε τις συντεταγμένες του κέντρου μάζας του συστήματος τη στιγμή και τη στιγμή t 1 όταν το φορτίο ζυγίζει σολθα κατέβει σε ύψος H.

Προς το παρόν:

,

Οπου , , Χ– αντίστοιχα, οι συντεταγμένες του κέντρου μάζας φορτίων βάρους g, g και μιας σφήνας που ζυγίζει Μσολ.

Ας υποθέσουμε ότι η σφήνα τη στιγμή του χρόνου κινείται προς τη θετική κατεύθυνση του άξονα Βόδικατά το ποσό μεγάλο, εάν το βάρος του φορτίου πέσει σε ύψος Ν.Τότε, προς το παρόν

επειδή τα φορτία μαζί με τη σφήνα θα μετακινηθούν προς μεγάλοπρος τα δεξιά και το φορτίο θα κινηθεί προς τα πάνω κατά μήκος της σφήνας. Αφού , τότε μετά από υπολογισμούς παίρνουμε

.

3.4. Ποσότητα κίνησης συστήματος

3.4.1. Υπολογισμός ορμής συστήματος

Η ορμή ενός υλικού σημείου είναι μια διανυσματική ποσότητα ίση με το γινόμενο της μάζας του σημείου και του διανύσματος της ταχύτητάς του

Μονάδα μέτρησης της ορμής -

Η ορμή ενός μηχανικού συστήματος είναι το διανυσματικό άθροισμα της ορμής επιμέρους πόντουςσυστήματα, δηλ.

Οπου Ν – αριθμός σημείων του συστήματος.

Η ορμή ενός μηχανικού συστήματος μπορεί να εκφραστεί ως προς τη μάζα του συστήματος Μκαι την ταχύτητα του κέντρου μάζας. Πραγματικά,

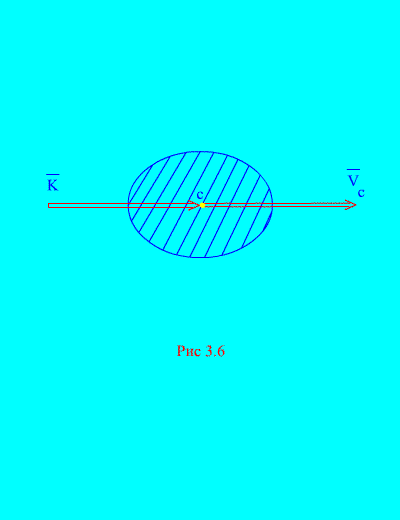
εκείνοι. Η ορμή του συστήματος είναι ίση με το γινόμενο της μάζας ολόκληρου του συστήματος και της ταχύτητας του κέντρου μάζας του.Η κατεύθυνση είναι ίδια με την κατεύθυνση (Εικ. 3.6)

Σε προβολές σε ορθογώνιους άξονες έχουμε

όπου , , είναι προβολές της ταχύτητας του κέντρου μάζας του συστήματος.

Εδώ Μ– μάζα του μηχανικού συστήματος. δεν αλλάζει όταν το σύστημα κινείται.

Αυτά τα αποτελέσματα είναι ιδιαίτερα βολικά στη χρήση κατά τον υπολογισμό των ποσοτήτων κίνησης των άκαμπτων σωμάτων.

Από τον τύπο (3.7) είναι σαφές ότι εάν ένα μηχανικό σύστημα κινείται με τέτοιο τρόπο ώστε το κέντρο μάζας του να παραμένει ακίνητο, τότε η ορμή του συστήματος παραμένει ίση με το μηδέν.

3.4.2. Στοιχειώδης και πλήρης ώθηση

Η δράση μιας δύναμης σε ένα υλικό σημείο με την πάροδο του χρόνου dtμπορεί να χαρακτηριστεί από μια στοιχειώδη παρόρμηση. Ολική ώθηση δύναμης με την πάροδο του χρόνου t, ή ώθηση δύναμης, που καθορίζεται από τον τύπο

ή σε προβολές σε συντεταγμένες άξονα

(3.8a)

Η μονάδα ώθησης δύναμης είναι .

3.4.3. Θεώρημα για τη μεταβολή της ορμής ενός συστήματος

Αφήστε τις εξωτερικές και εσωτερικές δυνάμεις να εφαρμοστούν στα σημεία του συστήματος. Στη συνέχεια για κάθε σημείο του συστήματος μπορούμε να εφαρμόσουμε τους διαφορικούς νόμους της κίνησης (3.3), έχοντας υπόψη ότι :

.

Αθροίζοντας όλα τα σημεία του συστήματος, παίρνουμε

Από την ιδιότητα των εσωτερικών δυνάμεων και εξ ορισμού έχουμε

(3.9)

Πολλαπλασιάζοντας και τις δύο πλευρές αυτής της εξίσωσης με dt, λαμβάνουμε ένα θεώρημα για τη μεταβολή της ορμής σε διαφορική μορφή:

, (3.10)

εκείνοι. η διαφορική ορμή ενός μηχανικού συστήματος είναι ίση με το διανυσματικό άθροισμα των στοιχειωδών παλμών όλων των εξωτερικών δυνάμεων που δρουν σε σημεία του μηχανικού συστήματος.

Υπολογισμός του ολοκληρώματος και των δύο πλευρών (3.10) σε βάθος χρόνου από 0 έως t, παίρνουμε το θεώρημα σε πεπερασμένη ή ακέραια μορφή

(3.11)

Σε προβολές στους άξονες συντεταγμένων θα έχουμε

Αλλαγή της ορμής ενός μηχανικού συστήματος με την πάροδο του χρόνουt, ισούται με το διανυσματικό άθροισμα όλων των παλμών των εξωτερικών δυνάμεων που δρουν σε σημεία του μηχανικού συστήματος κατά τον ίδιο χρόνο.

Παράδειγμα 4.Βάρος φορτίου Μ κατεβαίνει το κεκλιμένο επίπεδοαπό μια κατάσταση ηρεμίας υπό την επίδραση μιας δύναμης φά, ανάλογο με το χρόνο: , όπου (Εικ. 3.7). Τι ταχύτητα θα αποκτήσει το σώμα μετά t δευτερόλεπτα μετά την έναρξη της κίνησης, εάν ο συντελεστής τριβής ολίσθησης του φορτίου στο κεκλιμένο επίπεδο είναι ίσος με φά.

Λύση.Ας απεικονίσουμε τις δυνάμεις που εφαρμόζονται στο φορτίο: mg – δύναμη βαρύτητας φορτίου, Νείναι η κανονική αντίδραση του επιπέδου, είναι η δύναμη τριβής ολίσθησης του φορτίου στο επίπεδο, και . Η κατεύθυνση όλων των δυνάμεων φαίνεται στο (Εικ. 3.7).

Ας κατευθύνουμε τον άξονα Χκατά μήκος του κεκλιμένου επιπέδου προς τα κάτω. Ας γράψουμε το θεώρημα για τη μεταβολή της ορμής (3.11) στην προβολή στον άξονα Χ:

(ΕΝΑ)

Σύμφωνα με την προϋπόθεση, επειδή την αρχική στιγμή το φορτίο ήταν σε ηρεμία. Το άθροισμα των προβολών των παλμών όλων των δυνάμεων στον άξονα x είναι ίσο με

Ως εκ τούτου,

,

.

3.4.4. Νόμοι διατήρησης της ορμής

Οι νόμοι διατήρησης λαμβάνονται ως ειδικές περιπτώσεις του θεωρήματος της μεταβολής της ορμής. Δύο ειδικές περιπτώσεις είναι δυνατές.

· Αν το διανυσματικό άθροισμα όλων των εξωτερικών δυνάμεων που ασκούνται στο σύστημα είναι ίσο με μηδέν, δηλ. , τότε από το θεώρημα προκύπτει (3.9) , Τι ,

εκείνοι. αν το κύριο διάνυσμα των εξωτερικών δυνάμεων του συστήματος είναι μηδέν, τότε το μέγεθος της κίνησης του συστήματος είναι σταθερό σε μέγεθος και κατεύθυνση.

· Εάν η προβολή του κύριου διανύσματος εξωτερικών δυνάμεων σε οποιονδήποτε άξονα συντεταγμένων είναι ίση με μηδέν, για παράδειγμα Ox, δηλ. , τότε η προβολή της ορμής σε αυτόν τον άξονα είναι σταθερή τιμή.

Ας εξετάσουμε ένα παράδειγμα εφαρμογής του νόμου της διατήρησης της ορμής.

Παράδειγμα 5.Ένα βαλλιστικό εκκρεμές είναι ένα σώμα μάζας που αιωρείται σε ένα μακρύ νήμα (Εικ. 3.8).

Μια σφαίρα μάζας, που κινείται με ταχύτητα Vκαι χτυπώντας ένα ακίνητο σώμα, κολλάει σε αυτό, και το σώμα παρεκκλίνει. Ποια ήταν η ταχύτητα της σφαίρας αν το σώμα ανέβαινε σε ύψος η ?

Λύση.Αφήστε το σώμα με την κολλημένη σφαίρα να αποκτήσει ταχύτητα. Στη συνέχεια, χρησιμοποιώντας το νόμο της διατήρησης της ορμής κατά την αλληλεπίδραση δύο σωμάτων, μπορούμε να γράψουμε .

Η ταχύτητα μπορεί να υπολογιστεί χρησιμοποιώντας το νόμο της διατήρησης της μηχανικής ενέργειας . Επειτα . Ως αποτέλεσμα βρίσκουμε

.

Παράδειγμα 6. Το νερό εισέρχεται σε ένα στατικό κανάλι (Εικ. 3.9)μεταβλητή διατομή με ταχύτητα υπό γωνία ως προς την οριζόντια. περιοχή διατομής του καναλιού στην είσοδο. η ταχύτητα του νερού στην έξοδο από το κανάλι κάνει γωνία με τον ορίζοντα.

Προσδιορίστε την οριζόντια συνιστώσα της αντίδρασης που έχει το νερό στα τοιχώματα του καναλιού. Πυκνότητα νερού .

Λύση.Θα προσδιορίσουμε την οριζόντια συνιστώσα της αντίδρασης που ασκείται από τα τοιχώματα του καναλιού στο νερό. Αυτή η δύναμη είναι ίση σε μέγεθος και αντίθετη σε πρόσημο με την επιθυμητή δύναμη. Έχουμε, σύμφωνα με (3.11a),

. (ΕΝΑ)

Υπολογίζουμε τη μάζα του όγκου του υγρού που εισέρχεται στο κανάλι κατά τη διάρκεια του χρόνου t:

Καλείται η τιμή rAV 0 δεύτερη μάζα - η μάζα του υγρού που ρέει μέσα από οποιοδήποτε τμήμα του σωλήνα ανά μονάδα χρόνου.

Η ίδια ποσότητα νερού φεύγει από το κανάλι την ίδια ώρα. Οι αρχικές και τελικές ταχύτητες δίνονται στη συνθήκη.

Ας υπολογίσουμε σωστη πλευραισότητα (α) που καθορίζει το άθροισμα των προβολών στον οριζόντιο άξονα των εξωτερικών δυνάμεων που ασκούνται στο σύστημα (νερό). Η μόνη οριζόντια δύναμη είναι η οριζόντια συνιστώσα της προκύπτουσας αντίδρασης τοιχώματος Rx. Αυτή η δύναμη είναι σταθερή κατά τη διάρκεια της σταθερής κίνησης του νερού. Να γιατί

. (V)

Αντικαθιστώντας τα (β) και (γ) στο (α), παίρνουμε

3.5. Κινητική ροπή του συστήματος

3.5.1. Κύρια ροπή ορμής του συστήματος

Έστω το διάνυσμα ακτίνας ενός σημείου με τη μάζα του συστήματος σε σχέση με κάποιο σημείο Α, που ονομάζεται κέντρο (Εικ. 3.10).

Ορμή ορμής (κινητική ροπή) σημείου σε σχέση με το κέντρο Αονομάζεται διάνυσμα , καθορίζεται από τον τύπο

. (3.12)

Σε αυτή την περίπτωση, το διάνυσμα κατευθύνεται κάθετα στο επίπεδο που διέρχεται από το κέντρο ΕΝΑκαι διάνυσμα .

Ορμή ορμής (κινητική ροπή) σημείου σε σχέση με τον άξοναονομάζεται η προβολή σε αυτόν τον άξονα της ροπής ορμής ενός σημείου σε σχέση με οποιοδήποτε κέντρο που επιλέγεται σε αυτόν τον άξονα.

Η κύρια ροπή ορμής (κινητική ροπή) του συστήματος σε σχέση με το κέντρο Αονομάζεται ποσότητα

(3.13)

Η κύρια ροπή ορμής (κινητική ροπή) του συστήματος σε σχέση με τον άξοναονομάζεται προβολή σε αυτόν τον άξονα της κύριας ροπής ορμής του συστήματος σε σχέση με οποιαδήποτε επιλεγμένη σε αυτό κεντρικός άξονας.

3.5.2. Κινητική ροπή ενός περιστρεφόμενου άκαμπτου σώματος γύρω από τον άξονα περιστροφής

Ας ευθυγραμμίσουμε το σταθερό σημείο ΣΧΕΤΙΚΑ ΜΕσώμα που βρίσκεται στον άξονα περιστροφής ΣΧΕΤΙΚΑ ΜΕz, με την προέλευση του συστήματος συντεταγμένων Ohooz, οι άξονες των οποίων θα περιστρέφονται με το σώμα (Εικ. 3.11). Έστω το διάνυσμα ακτίνας ενός σημείου του σώματος σε σχέση με την αρχή των συντεταγμένων η προβολή του στον άξονα θα συμβολίζεται με , , . Διανυσματικές προβολές γωνιακή ταχύτητασώματα στον ίδιο άξονα συμβολίζουμε 0, 0, ().

Γειά σου! Ονομάζομαι Alexander Georgievich και είμαι επαγγελματίας δάσκαλος στη Μόσχα στην επιστήμη των υπολογιστών και στον προγραμματισμό. Έχετε συναντήσει κάποιο πρόβλημα που σχετίζεται με την κωδικοποίηση και έχετε μπερδευτεί σχετικά με τον αλγόριθμο για την επίλυσή του; Πρέπει επειγόντως να συναντηθείτεΚατάσταση Fanoκαι εγγραφείτε για ιδιαίτερα μαθήματα μαζί μου. Στα μαθήματά μου επικεντρώνομαι στην επίλυση θεματικών απλών και σύνθετων ασκήσεων.

Ποιο είναι το νόημα της άμεσης συνθήκης του Φάνου;

Κατάσταση Fanoπήρε το όνομά του από τον δημιουργό του, τον Ιταλοαμερικανό επιστήμονα Robert Fano. Η συνθήκη είναι απαραίτητη στη θεωρία κωδικοποίησης κατά την κατασκευή ενός αυτοτερματιζόμενου κώδικα. Δεδομένης της διαφορετικής ορολογίας, ένας τέτοιος κωδικός ονομάζεται κωδικός προθέματος.

Διατυπώ αυτή η συνθήκημπορεί να γίνει ως εξής: " κανένας μια κωδική λέξηδεν μπορεί να λειτουργήσει ως αρχή οποιασδήποτε άλλης κωδικής λέξης».

Από μαθηματική άποψη, η συνθήκη μπορεί να διατυπωθεί ως εξής: εάν ο κωδικός περιέχει τη λέξηB, μετά για οποιαδήποτε μη κενή συμβολοσειράΗ λέξη C BC δεν υπάρχει στον κώδικα».

Τι σημαίνει η αντίστροφη συνθήκη Fano;

Υπάρχει επίσης ένας αντίστροφος κανόνας Fano, η διατύπωση του οποίου είναι η εξής: καμία κωδική λέξη δεν μπορεί να λειτουργήσει ως το τέλος οποιασδήποτε άλλης κωδικής λέξης».

Από μαθηματική άποψη, η αντίστροφη συνθήκη μπορεί να διατυπωθεί ως εξής: εάν ο κωδικός περιέχει τη λέξη B, τότε για οποιαδήποτε μη κενή συμβολοσειρά C η λέξη CB δεν υπάρχει στον κωδικό».

Πρακτική εφαρμογή της συνθήκης Fano

Ας σκεφτούμε τηλεφωνικοί αριθμοί V παραδοσιακή τηλεφωνία. Εάν ο αριθμός "102" υπάρχει ήδη, τότε ο αριθμός "1029876" απλά δεν θα εκδοθεί. Εάν καλέσετε τα τρία πρώτα ψηφία, το PBX σταματά να αναγνωρίζει και να δέχεται όλα τα άλλα ψηφία, συνδέοντας τον συνδρομητή με τον αριθμό 102. Ωστόσο, αυτός ο κανόνας δεν ισχύει για τους χειριστές κινητές επικοινωνίες. Αυτό οφείλεται στο γεγονός ότι για να καλέσετε έναν αριθμό πρέπει να πατήσετε το αντίστοιχο πλήκτρο, το οποίο είναι κυρίως το πλήκτρο με την πράσινη εικόνα Ακουστικό. Για το λόγο αυτό, οι αριθμοί «102», «1020» και «1029876» μπορούν να υπάρχουν και να εκχωρηθούν σε διαφορετικούς παραλήπτες.

Το έργο:δίνεται μια ακολουθία που αποτελείται από τα γράμματα «Α», «Β», «Γ», «Δ» και «Ε». Για να κωδικοποιήσετε τη δεδομένη ακολουθία, μια ανομοιόμορφη δυάδικος κώδικας, με το οποίο μπορείτε να εφαρμόσετε ξεκάθαρη αποκωδικοποίηση.

Ερώτηση: Είναι δυνατόν ένα από τα σύμβολα να συντομεύσει το μήκος της κωδικής λέξης με τέτοιο τρόπο ώστε να διατηρηθεί η δυνατότητα σαφούς αποκωδικοποίησης; Σε αυτήν την περίπτωση, οι κωδικοί των υπολοίπων συμβόλων θα πρέπει να παραμείνουν αμετάβλητοι.

Λύση: για να διατηρηθεί η δυνατότητα αποκωδικοποίησης, αρκεί η συμμόρφωση με απευθείας ή αντίστροφηΣυνθήκες Fano. Ας πραγματοποιήσουμε έναν διαδοχικό έλεγχο των επιλογών 1, 3 και 4. Εάν καμία από τις επιλογές δεν είναι κατάλληλη, η σωστή απάντηση θα είναι η επιλογή 2 (δεν είναι δυνατή).

Επιλογή 1. Κωδικός: A - 00, B - 01, C - 011, D - 101 και E - 111. Απευθείας Κατάσταση Fanoδεν εκτελείται: ο κωδικός του χαρακτήρα "B" συμπίπτει με την αρχή του κωδικού του χαρακτήρα "C". Ο αντίστροφος κανόνας Fano δεν ισχύει: ο κωδικός του χαρακτήρα "B" συμπίπτει με το τέλος του κωδικού του χαρακτήρα "D". Η επιλογή δεν είναι κατάλληλη.

Επιλογή 3. Κωδικός: A - 00, B - 010, C - 01, D - 101, και E - 111. Απευθείας Κατάσταση Fanoδεν εκτελείται: ο κωδικός του χαρακτήρα "C" συμπίπτει με την αρχή του κωδικού του χαρακτήρα "B". Η αντίστροφη συνθήκη επίσης δεν ικανοποιείται: ο κωδικός του χαρακτήρα "C" συμπίπτει με το τέλος του κωδικού του χαρακτήρα "D". Η επιλογή δεν είναι κατάλληλη.

Επιλογή 4. Κωδικός: A - 00, B - 010, C - 011, D - 01 και E - 111. Απευθείας Κατάσταση Fanoδεν εκτελείται: ο κωδικός του χαρακτήρα "D" συμπίπτει με την αρχή του κωδικού των χαρακτήρων "B" και "C". Ωστόσο, τηρείται ο αντίστροφος κανόνας Fano: ο κωδικός του χαρακτήρα "D" δεν συμπίπτει με το τέλος του κωδικού όλων των άλλων χαρακτήρων. Για το λόγο αυτό, η επιλογή είναι κατάλληλη.

Αφού ελέγξετε τις επιλογές για την επίλυση του προβλήματος για συμμόρφωση με την άμεση και την αντίστροφη Κατάσταση Fano, διαπιστώθηκε ότι η επιλογή 4 είναι σωστή.

Απάντηση: 4

Και τώρα σας προτείνω να εξοικειωθείτε με τη λύση πολυμέσων στο πρόβλημα που προτάθηκε στην δοκιμαστική έκδοση του Unified State Exam στην επιστήμη των υπολογιστών και στις ΤΠΕ. Παρεμπιπτόντως, αυτή η εργασίααναφέρεται στο είδος των προβλημάτων που επιλύονται χρησιμοποιώντας Συνθήκες Fano.

Έχετε ακόμα ερωτήσεις;

Εάν μετά την ανάγνωση αυτής της δημοσίευσης εξακολουθείτε να έχετε κάποιες ερωτήσεις, παρεξηγήσεις ή θέλετε να ενοποιήσετε το υλικό που έχετε καλύψει πρακτικές λύσεις, στη συνέχεια τηλεφωνήστε και εγγραφείτε μαζί μου για ιδιαίτερα μαθήματα πληροφορικής και ΤΠΕ.

Εργασία 31. Ανομοιόμορφοι κωδικοί. Κατάσταση Fano

5-54 Για να κωδικοποιήσουμε μια συγκεκριμένη ακολουθία που αποτελείται από τα γράμματα A, B, C, D και D, αποφασίσαμε να χρησιμοποιήσουμε έναν μη ομοιόμορφο δυαδικό κώδικα, ο οποίος μας επιτρέπει να αποκωδικοποιήσουμε ξεκάθαρα τη δυαδική ακολουθία που εμφανίζεται στην πλευρά λήψης του. κανάλι επικοινωνίας. Για τα γράμματα A, B, C και D χρησιμοποιήθηκαν οι ακόλουθες κωδικές λέξεις: A - 001, B - 010, C - 000, D - 011.

Υποδείξτε ποια κωδική λέξη από αυτές που αναφέρονται παρακάτω μπορεί να χρησιμοποιηθεί για την κωδικοποίηση του γράμματος D.

Ο κωδικός πρέπει να ικανοποιεί την ιδιότητα της ξεκάθαρης αποκωδικοποίησης. Εάν μπορούν να χρησιμοποιηθούν περισσότερες από μία κωδικές λέξεις, εισαγάγετε τη συντομότερη.

1) 00 2) 01 3) 0000 4) 101

5-85. Για την κωδικοποίηση μιας συγκεκριμένης ακολουθίας που αποτελείται από τα γράμματα U, CH, E, N, I και K, χρησιμοποιείται μη ομοιόμορφη δυαδική κωδικός προθέματος. Εδώ είναι ο κωδικός: U – 000, Ch – 001, E – 010, N – 100, I – 011, K – 11. Είναι δυνατόν να συντομεύσετε το μήκος της κωδικής λέξης για ένα από τα γράμματα έτσι ώστε ο κωδικός να εξακολουθεί να παραμένει πρόθεμα; Οι κωδικοί των υπόλοιπων γραμμάτων δεν πρέπει να αλλάξουν. Επιλέγω σωστή επιλογήαπάντηση.

Σημείωση. Ένας κωδικός προθέματος είναι ένας κώδικας στον οποίο καμία κωδική λέξη δεν είναι η αρχή μιας άλλης. Τέτοιοι κώδικες καθιστούν δυνατή την ξεκάθαρη αποκωδικοποίηση της προκύπτουσας δυαδικής ακολουθίας.

1) η κωδική λέξη για το γράμμα Ε μπορεί να συντομευτεί σε 01

2) η κωδική λέξη για το γράμμα Κ μπορεί να μειωθεί σε 1

3) η κωδική λέξη για το γράμμα N μπορεί να μειωθεί σε 10

4) Αυτό είναι αδύνατο

5-94. Για να κωδικοποιήσουν μια συγκεκριμένη ακολουθία που αποτελείται από τα γράμματα A, B, C, D, αποφάσισαν να χρησιμοποιήσουν έναν μη ομοιόμορφο δυαδικό κώδικα που ικανοποιεί τη συνθήκη Fano. Για το γράμμα Α χρησιμοποιήθηκε η κωδική λέξη 1, για το γράμμα Β χρησιμοποιήθηκε η κωδική λέξη 011. Ποιο είναι το μικρότερο δυνατό συνολικό μήκος και των τεσσάρων κωδικών λέξεων;

5-74. Μηνύματα που περιέχουν μόνο 4 γράμματα μεταδίδονται μέσω του καναλιού επικοινωνίας: E, H, O, T. Σε οποιοδήποτε μήνυμα, τα περισσότερα γράμματα είναι O, το επόμενο πιο κοινό γράμμα είναι το E, μετά το N. Το γράμμα T είναι λιγότερο κοινό από οποιοδήποτε άλλο . Για τη μετάδοση μηνυμάτων, πρέπει να χρησιμοποιήσετε έναν μη ομοιόμορφο δυαδικό κώδικα που επιτρέπει τη σαφή αποκωδικοποίηση. τα μηνύματα πρέπει να είναι όσο το δυνατόν πιο σύντομα. Ο κρυπτογράφος μπορεί να χρησιμοποιήσει έναν από τους κωδικούς που αναφέρονται παρακάτω. Ποιον κωδικό να επιλέξει;

1) E – 0, N – 1, O – 00, T – 11 2) O – 1, N – 0, E – 01, T – 10

3) E – 1, N – 01, O – 001, T – 000 4) O – 0, N – 10, E – 111, T – 110

5-105. Τα μηνύματα μεταδίδονται μέσω του καναλιού επικοινωνίας, καθένα από τα οποία περιέχει 15 γράμματα A, 10 γράμματα B, 6 γράμματα C και 4 γράμματα G (δεν υπάρχουν άλλα γράμματα στα μηνύματα). Κάθε γράμμα κωδικοποιείται ως δυαδική ακολουθία. Κατά την επιλογή του κωδικού, ελήφθησαν υπόψη δύο απαιτήσεις:

α) καμία κωδική λέξη δεν είναι η αρχή μιας άλλης (αυτό είναι απαραίτητο για να επιτρέπει ο κώδικας ξεκάθαρη αποκωδικοποίηση).

β) το συνολικό μήκος του κωδικοποιημένου μηνύματος πρέπει να είναι όσο το δυνατόν μικρότερο.

Ποιον κώδικα από τους παρακάτω θα πρέπει να επιλέξετε για να κωδικοποιήσετε τα γράμματα A, B, C και D;

1) A:1, B:01, C:001, D:111

2) Α:1, Β:01, Γ:10, Δ:111

3) A:00, B:01, C:10, D:11

4) Α:100, Β:101, Γ:11, Δ:0

5-102. Υπάρχουν 10 διαφορετικά γράμματα στο μήνυμα. Κατά τη μετάδοσή του, χρησιμοποιείται ένας ανομοιόμορφος δυαδικός κώδικας προθέματος. Οι κωδικοί των τριών γραμμάτων είναι γνωστοί: 11, 100, 101. Οι κωδικοί των υπόλοιπων επτά γραμμάτων έχουν το ίδιο μήκος. Ποιο είναι το ελάχιστο συνολικό μήκος και των 10 κωδικών λέξεων;

5-104. Το μήνυμα περιέχει 50 γράμματα A, 30 γράμματα B, 20 γράμματα C και 5 γράμματα G. Κατά τη μετάδοσή του, χρησιμοποιήθηκε ένας ανομοιόμορφος δυαδικός κωδικός προθέματος, ο οποίος κατέστησε δυνατή τη λήψη του ελάχιστου μήκους του κωδικοποιημένου μηνύματος. Πώς είναι σε bits;

Μηνύματα που περιέχουν μόνο πέντε γράμματα μεταδίδονται μέσω του καναλιού επικοινωνίας: A, B, C, D, E. Για τη μετάδοση, χρησιμοποιείται ένας δυαδικός κώδικας που επιτρέπει τη σαφή αποκωδικοποίηση. Για τα γράμματα A, B, C χρησιμοποιούνται οι ακόλουθες κωδικές λέξεις: A – 111, B – 0, C – 100.

Καθορίστε τη συντομότερη κωδική λέξη για το γράμμα D, στην οποία ο κωδικός θα επιτρέπει σαφή αποκωδικοποίηση. Εάν υπάρχουν πολλοί τέτοιοι κωδικοί, υποδείξτε τον κωδικό με τον μικρότερο αριθμητική αξία.

9-1-23. Μετά τη μετατροπή ράστερ 256-χρωμάτων αρχείο γραφικώνστη μορφή 16 χρωμάτων το μέγεθός του μειώθηκε κατά 15 KB. Ποιο ήταν το μέγεθος αρχείο προέλευσηςσε KB;

9-1-25. Μετά τη μετατροπή του αρχείου γραφικών ράστερ, ο όγκος του μειώθηκε κατά 1,5 φορές. Πόσα χρώματα υπήρχαν στην παλέτα αρχικά, αν ελήφθη μετά τη μετατροπή εικόνα ράστερη ίδια ανάλυση σε μια παλέτα 16 χρωμάτων;

13-37. Κατά την εγγραφή στο σύστημα υπολογιστήΣε κάθε χρήστη εκδίδεται ένα αναγνωριστικό που αποτελείται από 8 χαρακτήρες, ο πρώτος και ο τελευταίος από τους οποίους είναι ένα από τα 18 γράμματα και τα υπόλοιπα είναι αριθμοί (10 επιτρέπονται δεκαδικά ψηφία). Κάθε τέτοιο αναγνωριστικό σε πρόγραμμα υπολογιστήγράφεται με τον ελάχιστο δυνατό και τον ίδιο ακέραιο αριθμό byte (χρησιμοποιείται κωδικοποίηση χαρακτήρα προς χαρακτήρα· όλοι οι αριθμοί κωδικοποιούνται με τον ίδιο και ελάχιστο δυνατό αριθμό bit, όλα τα γράμματα κωδικοποιούνται επίσης με τον ίδιο και ελάχιστο δυνατό αριθμό bits). Προσδιορίστε την ποσότητα μνήμης σε byte που εκχωρείται από αυτό το πρόγραμμα για την εγγραφή 500 κωδικών πρόσβασης.

13-38. Κατά την εγγραφή στο μηχανογραφικό σύστημα που χρησιμοποιείται για την ομαδική Ολυμπιάδα, δίνεται σε κάθε μαθητή μοναδικό αναγνωριστικό– ένας ακέραιος από 1 έως 1000. Ο ίδιος και ελάχιστος δυνατός αριθμός bit χρησιμοποιείται για την αποθήκευση κάθε αναγνωριστικού. Το αναγνωριστικό ομάδας αποτελείται από διαδοχικά καταγεγραμμένα αναγνωριστικά μαθητών και 8 επιπλέον κομμάτια. Το σύστημα χρησιμοποιεί τον ίδιο και ελάχιστο αριθμό byte για την καταγραφή κάθε αναγνωριστικού εντολής. Όλες οι ομάδες έχουν ίσο αριθμό συμμετεχόντων. Πόσα μέλη υπάρχουν σε κάθε ομάδα εάν χρειάζονται 180 byte για να αποθηκεύσετε τα αναγνωριστικά των 20 ομάδων που συμμετέχουν;

13-50. Κατά την εγγραφή σε ένα σύστημα υπολογιστή, σε κάθε χρήστη δίνεται ένας κωδικός πρόσβασης που αποτελείται από 15 χαρακτήρες και περιέχει μόνο χαρακτήρες από το σύνολο των 12 χαρακτήρων: A, B, C, D, E, F, G, H, K, L, M, N. Στη βάση δεδομένων Τα δεδομένα για την αποθήκευση πληροφοριών για κάθε χρήστη έχουν τον ίδιο και ελάχιστο δυνατό ακέραιο αριθμό byte. Σε αυτή την περίπτωση, χρησιμοποιείται η κωδικοποίηση των κωδικών πρόσβασης ανά χαρακτήρα, όλοι οι χαρακτήρες κωδικοποιούνται με τον ίδιο και ελάχιστο δυνατό αριθμό bit. Εκτός από τον ίδιο τον κωδικό πρόσβασης, στο σύστημα αποθηκεύονται πρόσθετες πληροφορίες για κάθε χρήστη, για τον οποίο εκχωρείται ένας ακέραιος αριθμός byte. αυτός ο αριθμός είναι ο ίδιος για όλους τους χρήστες. Για την αποθήκευση πληροφοριών για 20 χρήστες, απαιτήθηκαν 300 byte. Πόσα byte διατίθενται για αποθήκευση Επιπλέον πληροφορίεςπερίπου ένας χρήστης; Στην απάντησή σας, σημειώστε μόνο έναν ακέραιο αριθμό - τον αριθμό των byte.

16-165. Εννοια αριθμητική έκφραση: 9 22 + 3 66 – 18 γραμμένο στο βασικό 3 αριθμητικό σύστημα Πόσα ψηφία «2» υπάρχουν σε αυτόν τον συμβολισμό;